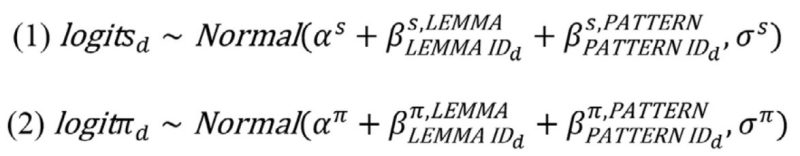Rate variation in language change: Toward distributional phylogenetic modeling

Abstract

Since the advent of phylogenetic linguistics, researchers have used a large number of phylogenetic comparative methods adapted from computational biology to model and analyze the dynamics of change of a wide range of linguistic features. Models of this sort vary in complexity; the simplest models of change assume homogeneity of transition rates within families, while state-of-the-art models of heterotachy allow transition rates to vary across lineages within a family. In this contribution, I review a range of applications of biological models of rate variation to questions in diachronic linguistics and highlight some models from computational biology that have remained largely overlooked by linguists. Building off of these and other biological models, I sketch out a program for what I term DISTRIBUTIONAL PHYLOGENETIC MODELING, inspired by an analogous recently proposed family of hierarchical Bayesian models. I report the results of some work in progress carried out within this framework and present a case study illustrating the flexibility of the approach.

Introduction

Despite the longstanding recognition of a number of parallels between biological and linguistic change, linguistics arguably lags behind biology in developing tractable quantitative models capable of testing hypotheses regarding the nature of change. While a number of computational biological models can be extended to questions regarding language change, diachronic linguistics in general has proved hesitant in adopting these models wholesale. Some of the qualms involved are justified: despite analogs between biological and linguistic evolution, the two fields often have different conceptions of the ways in which the features under study change. At the same time, phylogenetic models are increasingly designed with linguistic questions in mind, and as historical linguistics becomes more technically inclined, specialists in the field can assume a primary role in the development of such models. Popular models for categorical data types assume that features change according to a continuous-time Markov (CTM) process, a stochastic process parameterized by so-called transition rates, which characterize not only the speed with which transitions between feature values occur but also long-term trends towards particular values.

In this contribution, I probe the flexibility of standard biological models of transition rate variation with respect to addressing questions in linguistics. I provide (perhaps unsurprising) evidence that the biological term HETEROTACHY, although explicitly defined as RATE variation in a large number of publications—and thus suggesting models which allow transition rates to vary across different regimes of change with relative freedom—implicitly carries the meaning of variation in SPEED (and not in other properties of transition rates) in most of the biological literature surveyed. I review a range of applications of these models to questions in linguistics and explore the range of questions that such models are capable of answering. Additionally, I draw attention to a small number of biological methods that model the joint co-evolution of phenotypic and genetic traits but have gone largely unnoticed in linguistics, possibly due to their difficulty of implementation and a lack of recognition of the parallels between the phenomena described and comparable linguistic questions.

Taking these models as a starting point, I sketch out a framework that I term DISTRIBUTIONAL PHYLOGENETIC MODELING, which allows different properties of transition rates to vary according to different predictors, across features or lineages. This terminology pays homage to the newly developed framework of distributional statistical modeling, a family of regression models where both the expected location and dispersion of a response value can vary across predictor values. In a similar vein, distributional phylogenetic modeling assesses the effect of different predictors on a binary feature’s speed of change (the frequency with which transitions occur regardless of the direction of transition), and stationary probability (the long-term preference for a particular feature value). Some results of ongoing work in this framework are presented; additionally, I provide a case study showing how a distributional approach can potentially detect the role of areality in change in prosodic systems. I conclude by adumbrating additional potential applications for this method and discussing some challenges in generalizing this approach to non-binary data types.

Rate variation in biological and linguistic change

A number of biological models account for a phenomenon known as HETEROTACHY, derived from Greek takhus ‘swift’ and defined at times as speed variation (Lopez et al. 2002) but also in a large number of publications as rate variation (e.g., Meade and Pagel 2008: 30). Models of heterotachy allow properties of trait evolution to vary according to different regimes, across features and/or within phylogenies. However, from the concise definition given above, there is ambiguity regarding the exact quantities that vary across regimes — is there variation in the rate of change, i.e., the overall speed with which the system changes, or in transition rates more generally, which control not only the speed of the system but preferences for individual states? For phylogenetic linguistics, models which account for a broader understanding of rate variation are essential, as both properties of change are of importance to the field, as well as the extent to which dynamics of change vary as a function of different predictor variables. Below, I assess the extent to which existing biological models fulfill these desiderata.

As far as speed of change is concerned, a large body of work argues that linguistic features change at different speeds under different circumstances: for instance, different languages display divergent rates of vocabulary replacement (Bergsland and Vogt 1962), pointing to different dynamics of lexical change in different phylogenetic lineages. A wellknown but controversial hypothesis argues that language change is characterized by regimes of equilibrium, involving slow change, and punctuation, involving rapid change (Dixon 1997; for a critical appraisal of this specific view, see Bowern 2006). Other work, some of it in a phylogenetic framework, links different rates and trends in language change to differences in population size, different societal dynamics, and differences in social isolation (Nettle 1999; Greenhill et al. 2018). Additionally, a large body of research explores the role of large-scale language contact in accelerating language change (McWhorter 2007), particularly in extreme cases such as the formation of pidgins and creoles.

In addition to differences in the speed of change, regimes of language change can differ in terms of a preference for a given feature state and are thus characterized by different long-term biases toward feature values. These preferences may depend on another linguistic feature or one or more extra-linguistic features. It is argued, for instance, that labiodental sounds like f and v became easier to pronounce following changes to bite configuration associated with shifts in subsistence patterns and diet, and were thus more likely to be used as speech sounds (Blasi et al. 2019). Anatomical research also suggests that the click sounds found in languages of southern Africa are a relatively recent response to changes in physiology (Dediu et al. 2017, 2021; Moisik and Dediu 2017). It is additionally argued that social isolation is linked to the maintenance of linguistic complexity, with simplification brought about by adult second-language learners (Bentz and Winter 2013; Trudgill 2001). As in the case of phonological inventories, environmental factors have also been invoked as an influence on static sound patterns within languages. For instance, it has been claimed that languages spoken in drier climates use fewer vowels (Everett 2017) and that the same pattern holds for languages spoken in colder climates (Maddieson 2018), due to the fact that dry air creates articulatory problems for phonation needed to produce vowels, and high temperatures degrade the high-frequency spectral information helpful in perceiving consonant clusters. In addition to environmental factors, genetic factors have been implicated in biases toward linguistic tone (Dediu 2021). Studies demonstrate robustly that tonal languages are spoken in regions of higher humidity (Everett et al. 2015; Roberts 2018), due to the fact that lower jitter in fundamental frequency, a property of humid environments, makes it easier to stabilize fundamental frequency and exapt it for linguistic purposes. Hypotheses that posit the direct influence of the environment on sound patterns are highly controversial (Haynie 2014; Urban 2020), as it is difficult to tease apart the correlated influence of environment, areality, and genetics, and it has been argued in recent years that hypotheses regarding the influence of the environment on sound patterns (Everett 2013) are better analyzed as sociolinguistic isolation (Urban and Moran 2021). Regardless of the factors involved, a growing body of evidence robustly attests that phylogenetic lineages are characterized by different regimes of change that vary both in the speed of change and preferences for individual features.

The quantitative turn in historical linguistics has seen an increase in the application of phylogenetic methodologies to questions in historical linguistics. A popular model for the evolution of categorical linguistic data assumes that features undergo state changes over a phylogeny (usually inferred a priori on the basis of lexical data) according to a continuous-time Markov (CTM) process. The transition rates of the process can be estimated (usually via Bayesian inference) and estimated values can be used to test hypotheses regarding the dynamics of change in the features in question. To date, the majority of applications of the CTM model in linguistics assume that transition rates between features or pairs of features do not vary within phylogenies (Carling and Cathcart 2021; Cathcart et al. 2020; Dunn et al. 2017; Haynie and Bowern 2016; Shirtz et al. 2021). If data from multiple families are analyzed, phylogenetic models are generally fitted separately for each family, with different rates for each family (Dediu 2010; Dunn et al. 2011).1 Although the rate homogeneity assumption may be overly simplistic, given the evidence for different rate regimes in language change mentioned above, this assumption has a number of advantages: given the relatively small number of parameters in rate-homogeneous models, they are computationally efficient to fit, and their restrictiveness may allow for less uncertainty in posterior estimates than in more elaborate models. Additionally, questions asked in the work cited here are in no way related to rate heterogeneity and are more concerned about exploring the long-term dynamics of feature change; recent work even finds support for rate homogeneity across rather than within families (Jäger and Wahle 2021). At the same time, rate heterogeneity, both across features and lineages, is central to a number of outstanding questions in linguistics, including those raised at the beginning of this section.

A number of well-known models of heterotachy account for variation in speed across evolving features as well as within phylogenies. Models accounting for within-phylogeny variation can be subdivided into models which assume variation to be fixed at the branch level, and those that allow multiple rate regimes to be visited on a single branch of a phylogeny. The latter type is best represented by the COVARION model, a prominent way of representing heterotachy (Fitch 1971; Tuffley and Steel 1998; Wang et al. 2007). A basic covarion model for binary data assumes a four-state CTM process with “hot” and “cold” regions characterized by normal and slow or nonexistent change. The system can transition from hot to cold regions or vice versa but change between presence and absence is more frequent in hot regions than in cold ones. The hidden rates model is a generalization of the covarion model that allows gain and loss rates to differ across rate regimes in a less constrained manner, not solely according to speed, and additionally can accommodate more than two rate classes (Beaulieu and O’Meara 2014).

Other alternatives to the covarion model assume that speed variation is fixed at the branch level (Heath et al. 2011; Pagel and Meade 2008). Unlike the covarion model, within-branch transitions between rate classes are not permitted.² At the same time, branch-level models are more flexible than covarion models in that it is straightforward to account for a greater number of rate regimes to an extent that would be computationally costly under a covarion model, as it would involve a high-dimensional rate matrix (Irvahn and Minin 2014). The models cited above allow variation in speed, but not necessarily in branch-level trends toward some feature value. Limiting variation to speed enables some computational tricks, as differences in speed can be modeled at the branch level by directly manipulating the branch length rather than the rates of the CTM process.

Similar methods are used to account for variation in rates across features. Huelsenbeck and Suchard (2007) allow the speed of change of different features to vary across speed classes by manipulating the total tree length across rate classes. A notable linguistic study allowing speeds to vary across branches and features is that of Greenhill et al. (2017), which analyzes change in lexical and morphosyntactic features in Austronesian, allowing speed variation across branches as well as features (the authors coestimate speeds of change along with language phylogenies, rather than assuming the phylogeny a priori).

Ultimately, an overwhelming number of off-the-shelf models of heterotachy account solely for variation in speeds of change. One obvious reason is the fact that methods of this sort are designed for modeling change in DNA sequences, where in most circumstances there are no clear biases towards particular bases (though see below). Another issue is the fact that models of this sort rely on Markov chain Monte Carlo (MCMC) methods, which must satisfy certain constraints in order to efficiently explore parameter space. Many MCMC methods suffer when exploring high-dimensional posteriors; hence, simpler models are easier to tune such that proposals are efficient. Models of this sort are readily available to linguists interested in speed variation, but not necessarily in other dynamics of change. Furthermore, these methods do not directly model the role of different linguistic and extra-linguistic predictors in explaining variation in the dynamics of change. One model capable of doing this is the Discrete model of correlated evolution (Pagel 1994), under which gain and loss rates for one feature vary freely according to the presence or absence of another feature; this model requires a binarized representation of both features.

Despite the fact that the most accessible models of heterotachy model only variation in speed and are thus not expressive enough to capture the full range of phenomena of interest to phylogenetic typology, other models, albeit less well-known ones, may be relevant to the needs of the subfield. There exist a number of biological models which jointly characterize the evolution of continuous phenotypic and discrete genetic traits across lineages within a phylogeny (see Bromham 2009; Bromham et al. 1996 on some relevant phenomena). These are overlooked in the phylogenetic linguistics literature, because at first blush there is no clear connection between the biological phenomena they capture and linguistic processes we may wish to model. Lartillot and Poujol (2011) model correlations between several phenotypic variables (maturity, mass, and longevity) and the ratio of nonsynonymous (i.e., transitions between nucleotides that alter the amino acid sequence of a protein) to synonymous substitutions. A handful of papers (Horvilleur and Lartillot 2014; Lartillot 2013) deal with so-called GC equilibrium or GC-biased gene conversion, a phenomenon where repairs to certain DNA mismatches may favor strong bases (G and C) over their weak counterparts (A and T), and possible extra-genetic correlates or determinants thereof. While it is challenging to find a direct analog in linguistics for the biological phenomena to which these methods are applied, the importance of models of this sort is clear: they provide a means of representing relationships between co-evolving continuous and discrete features off of which phylogenetic linguistic methods can build in order to explore how changes in a continuous extra-linguistic feature influences long-term preferences for values of a discrete linguistic feature, as well as its speed of change (although these models do not explicitly address speed) (Table 1).

Markov chain Monte Carlo (MCMC) implementations of the models described above are not straightforward to modify by researchers wishing to apply the models to non-biological data. Fortunately, specialists lacking the expertise to tune and modify MCMC algorithms for the purpose of efficient sampling can make use of an increasing set of offerings in the domain of probabilistic programming languages which require only a specification of the generative process thought to underlie the data. One such language is Stan (Carpenter et al. 2017), which uses an adaptive version of Hamiltonian Monte Carlo, a gradient-based method that avoids the random walk behavior of MCMC approaches, making it possible to infer larger numbers of parameters and employ flexible prior distributions over parameters. Recent sophisticated phylogenetic models have been implemented in Stan, including phylogenetic causal modeling (Ringen et al. 2021). Programming languages like Stan can be used to recast some of the models described above, in order to make them more flexible, with some limitations. A salient limitation of gradient-based probabilistic programming languages like Stan is that discrete parameters cannot be directly sampled, and must be marginalized, which is unfeasible under some circumstances. This rules out the possibility of modeling branch-specific rate classes, which involves an exponentially increasing enumeration of configurations of rate class membership across a phylogeny, and makes modeling feature-specific rate classes computationally costly for large numbers of features and rate classes. In what follows, we move away from the notion of discrete rate classes in favor of approaches that allow speeds and preferences to vary at both the branch level as a function of one or more predictors.

Distributional modeling

In this section, I motivate a method for assessing the effect of different predictors on multiple components of language change for binary linguistic features. Specifically, this method decouples transition rates into the overall speed of change, i.e., the scale of the change rate between feature states irrespective of the direction of change, and the stationary probability of feature presence, interpretable as the long-term preference for a given feature.

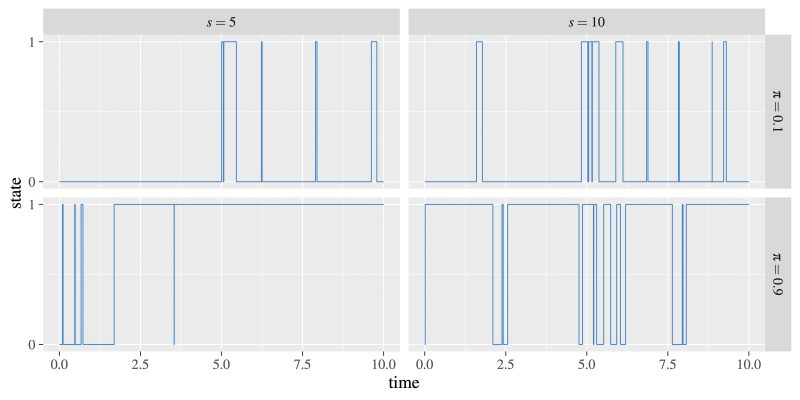
Under the standard view of a continuous-time Markov process for binary data, a feature arises and is lost according to a gain rate and a loss rate. Assuming a speed of change s and stationary probability π, the gain rate and loss rate can be rewritten as sπ and s(1 − π), respectively (see Fig. 1). This is the binary case of a general time-reversible model (Tavaré 1986), which parameterizes changes between multiple states in a continuous-time Markov chain according to stationary probabilities of state presence and exchange rates (identical to what I term the speed of change) between each pair of states. Simulated trajectories of change under binary CTM processes with different speeds and stationary probabilities are found in Figure 2.

Allowing both the speed of change and stationary probability of a feature to vary according to one or more predictors invites analogies with a recently proposed innovation in hierarchical Bayesian modeling, namely so-called DISTRIBUTIONAL MODELS, which allow both the location and scale of a regression model to vary as a function of predictor variables (Bürkner 2017), thus relaxing a number of assumptions found in classical linear regression, such as homoskedasticity. In the same vein, distributional phylogenetic modeling can allow us to understand which properties of change vary according to different predictor variables, both within and across features. A more refined understanding of whether certain extralinguistic predictors of change affect speed versus biases toward a particular feature value can be crucial to our understanding of language change. For instance, it could be the case that what appears to be the result of increases in complexity in regions of greater social isolation is simply an artifact of more rapid change in regions of less isolation. Decoupling these components of change provides a principled method for investigating hypotheses of this sort, both across lineages as well as linguistic features.

In what follows, I illustrate the results of work that investigates the role of different predictors in explaining variation in speed of change and stationary probability of presence at the featural level, using a large linguistic data set. Subsequently, I present the results of a case study that models differences in speed at the branch level as a function of an extralinguistic feature, namely geospatial dynamics.

Case study: Romance verbal morphology

Cathcart et al. (2022) conduct a study in a distributional phylogenetic framework of the evolution of stem alternations in Romance verbs. Stem alternations in Romance verb paradigms are of particular interest to diachronic linguistics (Esher 2016; Herce 2019; Maiden 2018, etc.). Romance verbal paradigms often exhibit so-called morphomic patterns constituting stem allomorphy that is neither phonologically nor semantically motivated. Despite their irregularity, these patterns are highly stable and are frequently extended to new verbs. The philological literature identifies three main types of stem alternations in Romance verbs, labeled N, L, and P(YTA); these can co-occur within verbal paradigms. The emergence of the N and L patterns occurred as a result of sound changes after Classical Latin but (largely) before the break-up of Romance into different languages. Unlike the other two patterns, the P pattern is inherited from Latin, stemming from a semantic distinction that is no longer present in modern Romance languages, leading to alternations that are arbitrary from the perspective of meaning.

Data from the Oxford Online Database of Romance Verb Morphology (Beniamine et al. 2020; Maiden et al. 2010) were manually coded according to whether or not they exhibited each of the three pattern types (which can co-occur within individual paradigms), yielding three possible lemma-pattern pairs per lemma in each language. In total, the data analyzed comprised 171 lemma-pattern pairs involving 66 lemmas from 67 Romance speech varieties (lemma-pattern pairs exhibiting no variation between the states present and absent were excluded). A Romance phylogeny was used to carry out distributional phylogenetic modeling, inferred using RevBayes (Höhna et al. 2016) on the basis of both automatically generated lexical cognacy data (Jäger 2018) and sound class data indicating speech sounds that are present in each variety Heggarty et al. (2019).

As morphomic pattern types can co-occur within the same lexeme’s verbal paradigm, each lemma-pattern pair is assumed to evolve independently according to a binary CTM process between the states PRESENT and ABSENT. The gain and loss rate of a lemma-pattern pair with index d ∈ {1,…,D} are π_ds_dρ and (1 − π_d)s_dρ. Here, s_dρ represents the speed of change for feature d, s_d being a multiplier of the global speed ρ. The global speed ρ ∼ Uniform(0,10) represents the global speed of change, which varies from feature to feature according to the multiplier s_d, and prevents changes from happening more frequently than once per century. The parameter π_d is the stationary probability for the lemma-pattern pair in question. For each feature, the likelihood P(x_d|s_d,π_d,ρ,Ψ) can be computed using Felsenstein’s pruning algorithm (Felsenstein 1981, 2004), where xd is a vector of values indicating the presence or absence of a given lemma-pattern pair in the languages in the data set, and Ψ is a phylogeny. Both the speed of change and stationary probability for each lemma-pattern pair can be modeled as a function of multiple predictors, making it possible to assess the effect of different factors on both speed and stationary probability. Both s and π are logit-normally distributed, as follows:

In each sampling statement, α represents an intercept, β^LEMMA represents the contribution of each lemma type, and β^PATTERN represents the contribution of each alternation type. The contribution of lemma type is modeled as a monotonic function (Bürkner and Charpentier 2020) of each lemma’s frequency in Latin texts. Pattern type is dummy-coded, modeling comparisons of the levels L and P to N, respectively. Normal(0,1) priors are placed over all model parameters in statements (1–2) with the exception of simplex parameters and standard deviations σ, which receive Dirichlet(1,…,1) and HalfNormal(0,1) priors, respectively. Posterior distributions for parameters are inferred using the R package CmdStanR (Gabry and Češnovar 2021). The resulting posterior coefficientsˇ for model predictors (given in Fig. 4) serve to clarify some aspects of morphological change that were previously poorly understood or underappreciated. Interestingly, none of the predictors have a decisive effect on the speed of change of a lemma-pattern pair, as 95% credible intervals for these parameters all overlap with zero. However, frequency has a decisive effect on the stationary probability of pattern presence (β^π,LEMMA). This result is interesting in light of a large body of research that links frequency of usage to speed of change in vocabulary replacement (Pagel et al. 2007, though see also Wilson et al. 2019). In the case of Romance verbal paradigms, lexical frequency does not explain variation in speed of change, but in other properties of change. A tentative interpretation of this result is that the loss versus maintenance of irregularity in less versus more frequent forms is not an accident brought about by the instability of less frequent forms, but rather reflects the evolutionary advantage of maintaining irregular patterns in highly frequent verbs. The distributional model developed can be straightforwardly extended to model branch-level trends in change (pertaining to both speed and preferences for general irregularity or specific irregular patterns) and can incorporate a wide range of predictors.

Case study: Stress systems of the world’s languages

In this section, I present the results of a case study designed to demonstrate the flexibility of a distributional approach in assessing the role of different predictors across multiple features and lineages. Importantly, the model I construct probes the influence of geospatial factors on across-lineage trends in change. Though highly preliminary at this stage, this work further advances phylogenetic linguistics in the direction of accounting for horizontal as well as vertical pressures in language change.

I apply the model developed to the question of change in stress systems. Languages differ widely in terms of the suprasegmental systems they exhibit. Language change can involve drastic transitions between types of prosodic behavior. For instance, Old Latin had fixed stress on initial syllables, whereas Classical Latin developed stress on penultimate or antepenultimate syllables, depending on vowel length (Penney et al. 2011); additionally, Old Chinese is believed to have lacked tone, yet lexical tone developed in later Chinese varieties via tonogenesis (Baxter 1992). Changes in prosodic systems are well studied. In particular, the emergence of tone is linked to voicing and other acoustic properties that may be enhanced by environmental and genetic factors. At the same time, many aspects of change in stress systems are not fully understood. While undoubtedly many factors are involved, language contact is frequently invoked as a source of prosodic change (Pronk 2018; Rice 2014). For instance, the presence of initial stress among genetically distantly related languages of Central Europe such as Hungarian and Czech is highly conspicuous, and usually attributed to contact. (Fig. 3)

As a means of assessing the role of geography in linguistic change, I jointly model the phylogeographic diffusion of language families along with a distributional CTM model of the evolution of features pertaining to prosody. I assume a relaxed random walk model (RRW) of phylogeography, under which geospatial diffusion takes place according to a process of Brownian motion, the scale of which exhibits branch-level variation. This model and some extensions serve as the standard for modeling linguistic migration (Gill et al. 2017; Lemey et al. 2010), and are shown to accurately capture properties of a language family’s spread when the process of spread involves expansion from a given point of origin, but not necessarily when wholesale migration from the point of origin has taken place (Neureiter et al. 2021); accordingly, the RRW and its extensions may not be appropriate for all of the world’s language families. The basic RRW employed in this paper is not sensitive to environmental features in the way that more sophisticated models are (Bouckaert et al. 2012, 2018; Koile et al. 2022).

I take branch-level diffusion rates as our key geospatial parameter of interest. These parameters model fluctuation in the speed of migration of different phylogenetic lineages. More rapid migration on the part of a speech community has the potential to bring speakers into contact with speakers of other languages, increasing the possibility of language shift among adults and rapid changes in typological profile. If this view is accurate, higher rates of geospatial diffusion should coincide with faster speeds of featural change on the same branch. This hypothesis — that the speed of geospatial diffusion has a positive effect on the speed of linguistic change — is perhaps simplistic, but the investigation carried out here opens the door for more nuanced studies of this broader question.

I use data from chapters 14–15 (Fixed Stress Locations and Weight-Sensitive Stress; Goedemans and van der Hulst 2013a, 2013b) of the World Atlas of Linguistic Structures (Dryer and Haspelmath 2013). The data were recoded into 12 binary traits (Antepenultimate, Initial, Penultimate, Second, Third, Ultimate, Left Edge, Left Oriented, Not Predictable, Right Edge, Right Oriented, Unbounded), removing redundant features logically dependent on other feature values. In theory, multiple stress types can co-occur within languages in different lexical strata, making a binary data type an appropriate representation for these feature values. Whether or not all features can be absent in a given language (e.g., in sign languages, in certain tone languages) gets further into the domain of theoretical analyses outside the scope of this paper (Duanmu 2004; Hyman 2006); this behavior would be a potentially unintended consequence of a binary data type.

To prepare the data for phylogenetic analysis, I used the workflow designed by Jäger and Wahle (2021). I merged each glottocode in the recoded WALS data with one or more corresponding taxa in the ASJP dataset (Wichmann et al. 2018). This expanded the 485 languages in the WALS sample into 779 ASJP taxa for which stress data are available. I inferred phylogenies for the families in the augmented data set. In sum, the augmented data contained taxa from 57 families, of which 13 con- tained only two members, as well as 55 taxa that were the sole representatives of their family. I limited my analyses to 698 languages from 44 families comprising more than 2 members. Data and code can be found at https://github.com/chundrac/phylogeneticTypology.

I fit three models of increasing complexity. The first of these (MODEL) assumes that each feature in the data set evolves in each phylogeny according to a global change rate and stationary probability. The second of these (MODEL-FAM) allows change rates and stationary probabilities for features to vary across families. The third of these (MODEL-FAM-GEO) builds upon MODEL-FAM, combining an RRW model of phylogeography with a CTM model of character evolution in order to detect fluctuation in the speed of change that may be explained by variability in rates of phylogeographic diffusion at the branch level. Under a time-homogeneous Brownian motion, displacement in a trait value between times s and t, x_t − x_s is normally distributed with a mean of 0 and a variance of σ(t − s), where σ is a parameter controlling the overall scale of diffusion. The RRW model multiplies σ by a branch-specific scale ρ_b for a branch with index _b, which allows for faster or slower displacement on different branches. This model allows change rates and stationary probabilities for features to vary across families, and also allows branch-level speeds of change to vary as a function of the phylogeographic diffusion rates of corresponding branches. A detailed model specification can be found in the Appendix.

Model comparison was carried out via Pareto-smoothed importance sampling leave-one-out (PSIS-LOO) cross-validation (Vehtari et al. 2017). Posterior samples (including log-likelihood values for each sample) were aggregated across all 10 posterior distributions. Differences in expected log predictive density (ELPD) values across models were calculated using the function loo compare in the R package loo (Vehtari et al. 2020). Below, we see differences in ELPD between each model and the model with the largest ELPD (the model in the first row), along with standard errors of the differences. In general, if the absolute difference is greater than two standard errors, the model with the higher ELPD is a decisively better fit to the data. I also carry out model stacking (Yao et al. 2017), which averages predictive distributions of different models to generate weights representing their relative predictive power; weights are provided below.

The diffusion-sensitive model is the best fit for the data, followed by the model with family-level rate variation. There is little support for the idea that universal trends alone account well for the variation in the data. A question arises as to why there is support for family-specific rate variation in this paper’s models, but not in the results of Jäger and Wahle (2021), who analyze Greenbergian word order correlations. A reason for this may be that models of the evolution of interdependent features capture global dynamics rooted in cognitive pressures, which hold across families. Here, we analyze the independent evolution of specific prosodic traits, which are preferred to different degrees in different phylogenies and linguistic areas, and are thus better characterized by evolutionary dynamics that vary across families.

For MODEL-FAM-GEO, I inspect the posterior distribution of the parameter β_GEO^s, which controls the effect of branch-level phylogeographic diffusion rates on branch-level speeds of change (see Fig. 4). 100% of samples are greater than zero, indicating decisive evidence for a positive effect of phylogeographic diffusion rate on the speed of linguistic change. This indicates that branches with faster speeds of migration tend to exhibit higher overall speeds of change for the linguistic features analyzed here. This result can be interpreted as evidence that change in prosodic features shows sensitivity to dynamics of geospatial change, indirectly pointing to the role of contact in language change.

This result is intriguing, although it should be evaluated with care. Conclusive acceptance of this result will hinge on careful model criticism in order to ensure that this result is not an artifact of some properties of the model that are incorrect. An important step, outside of the scope of this paper, is to inspect distributions of diffusion rates at the individual branch level to ensure that patterns dovetail with extra-linguistic information regarding individual languages’ dispersal. A preliminary inspection of the phylogeographic parameters, specifically, the inferred locations for proto-homelands (Fig. 5) of the different families in the sample, indicates some shortcomings and directions for improvement. Many of the inferred homeland locations do not reflect consensus views found in the literature: to mention only a few, the Indo-European homeland is inferred to be in Central Europe, which is not a serious candidate for the Indo-European Urheimat; the Austronesian homeland is inferred to be in Indonesia rather than Taiwan; the Turkic homeland is located further to the west than the traditional view holds it to be. It appears to be the case that inferred homeland locations are highly sensitive to biases in the linguistic sample: non-European Indo-European languages are underrepresented, as are Formosan Austronesian languages. Ancient and medieval languages that can serve to produce more plausible estimates of homeland locations are also missing from this data set. This issue can be alleviated in a number of ways. One approach might involve imposing relatively informative priors over homeland locations, based on proposals in the literature; this would be particularly helpful in situations where migration of speech communities rather than expansion has taken place. Another approach would be to estimate phylogenetic parameters on the basis of a larger tree than the subtrees for which typological data are available while estimating parameters of the CTM model on the basis of a smaller tree. It is worth noting that none of the trees used here are calibrated to produce realistically timed branch lengths, so the use of published trees with more accurate chronologies will aid this process as well (there is the risk that unrealistically shallow or deep chronologies for language phylogenies will respectively overestimate and underestimate phylogeographic diffusion rates, as the model will take languages to have undergone more or less migration over time than expected). Fitting family-level, as well as global and branch-level diffusion rate multipliers, might help to account for variation in chronologies among phylogenies that stems from modeling assumptions (cf. Chang et al. 2015). At the same time if different families have in fact undergone geographic dispersal at different overall rates, then fitting family-level rate multipliers might suppress meaningful effects of diffusion rate on linguistic change.

Yet another issue is the fact that for this paper, phylogeographic parameters and CTM parameters were co-inferred, with posterior parameters inferred on the basis of the joint distribution of the phylogeographic and CTM parameters. This has the potential to produce different results than a procedure in which phylogeographic parameters are first estimated on their own, with CTM parameters subsequently estimated on the basis of phylogeographic distributions (employing some form of measurement error). Just as phylogenetic comparative methods tend to treat the phylogenetic representation of taxa under study as a given, not to be coestimated with evolutionary dynamics of the data under study, so too might we wish to treat phylogeographic distributions as given quantities on the basis of which we wish to condition our models.

These issues aside, this case study serves as an important proof of concept for the integration of phylogeographic models and CTM models of linguistic evolution. Related approaches can investigate more direct questions regarding the role of geography in language change. Here, we looked only at the effect of diffusion rate on the speed of feature change, but this variable’s role in shaping trends toward simplification could be investigated as well (cf. Jing et al. 2022). Additionally, inferred longitude and latitude values for internal nodes of phylogenies in a sample can be incorporated into a CTM model of character evolution. These values could be used to detect spatial autocorrelation in branch-level fluctuation in speed or preferences for particular features in a data set. Under most circumstances, Gaussian Processes (Rasmussen and Williams 2006) are ideal for modeling spatial autocorrelation, given their flexibility. At the same time, they are computationally costly for large numbers of data points, as the covariance between each pair of data points must be computed. For phylogenetic samples like this paper’s, there are too many branches for this to be computationally feasible. A recently developed method approximates draws from a Gaussian Process using basis functions (Riutort-Mayol et al. 2020), which lowers the computational cost for large data sets. At the same time, this method requires several nontrivial decisions on the part of the user, such as the choice of the number of basis functions. A Gaussian Process-based approach may be more appropriate for targeted studies involving smaller numbers of phylogenies comprising languages spoken in the vicinity of each other.

Outlook

In the previous sections, I introduced distributional phylogenetic modeling, an approach that takes as its inspiration advances in hierarchical Bayesian modeling and builds off of biological models of the co-evolution of continuous and discrete traits. I showed how these models can be used to analyze rate variation across features as well as phylogenetic lineages, and demonstrated that by decoupling speed of change and stationary probability of feature presence, we can uncover the effects of different predictor variables on different components of change. It is hoped that this framework will be useful in further advancing our understanding of the relationship between different extralinguistic and linguistic variables, which are much discussed in the literature but generally analyzed in a regression framework, which does not explicitly model the diachronic dynamics of these relationships. For instance, if we are willing to assume that a language’s altitude, often taken as a proxy for social isolation (Nichols and Bentz 2019), evolves according to a stochastic process such as Brownian motion or variants thereof, we can assess whether decreases in altitude have an effect on linguistic complexity, as operationalized by some discrete feature. For other extra-linguistic features, such as population size and environmental data, simple models like Brownian motion are most likely not appropriate and may have to make use of historical data in order to make accurate estimates (e.g., Huebner 2020).

An issue of concern is the fact that the models presented here involve binary data, which can be straightforwardly parameterized according to the speed and stationary probability of the CTM process according to which the data are assumed to evolve. Extending this approach to non-binary data types requires some serious thought. The General Time-Reversible model (Tavaré 1986) explicitly models CTM processes for non-binary data according to the stationary probabilities of each state as well as exchange rates between each pair of states, representing the rate of change between each pair of states irrespective of its direction. Given this setup, it is straightforward to allow both speed and stationary probability to vary independently across rate regimes. At the same time, for K states, the GTR model contains K + (K(K – 1))/2 free parameters, in comparison to a CTM process involving independent rates between each pair of states, which would have K(K − 1) parameters. It is therefore possible that the GTR model is too restrictive to capture certain phenomena. This is to say nothing of the difficulties that may arise in interpreting the effects of predictors on different components of a more complex process of change.

Ultimately, while much ground has been broken in developing flexible models designed expressly for phylolinguistics, many tasks remain in fully understanding the diachronic pressures that shape synchronic linguistic distributions. It is hoped that with an increase in flexible approaches, we will move closer to this goal.

References

Baxter, W. H. 1992. A handbook of Old Chinese phonology. De Gruyter Mouton.

Beaulieu, J. M., and B. C. O’Meara. 2014. Hidden Markov models for studying the evolution of binary morphological characters. In Modern Phylogenetic Comparative Methods and Their Application in Evolutionary Biology: Concepts and Practice, ed. by L. Z. Garamszegi, pp. 395–408. Heidelberg, New York, Dordrecht, London: Springer.

Beniamine, S., M. Maiden, and E. Round. 2020. Opening the Romance verbal inflection dataset 2.0: a cldf lexicon. In Proceedings of The 12th Language Resources and Evaluation Conference, pp. 3027–3035.

Bentz, C., and B. Winter. 2013. Languages with more second language learners tend to lose nominal case. Language Dynamics and Change 3(1): 1–27.

Bergsland, K., and H. Vogt. 1962. On the validity of glottochronology. Current Anthropology 3(2): 115–153.

Blasi, D. E., S. Moran, S. R. Moisik, P. Widmer, D. Dediu, and B. Bickel. 2019. Human sound systems are shaped by post-Neolithic changes in bite configuration. Science 363(6432): 6432.

Bouckaert, R. R., C. Bowern, and Q. D. Atkinson. 2018. The origin and expansion of Pama-Nyungan languages across Australia. Nature ecology & evolution 2(4): 741–749.

Bouckaert, R., P. Lemey, M. Dunn, S. J. Greenhill, A. V. Alekseyenko, A. J. Drummond, R. D. Gray, M. A. Suchard, and Q. D. Atkinson. 2012. Mapping the origins and expansion of the Indo-European language family. Science 337(6097): 957–960.

Bowern, C. 2006. Punctuated equilibrium and language change. Encyclopedia of language and linguistics: 286–289.

Bromham, L. 2009. Why do species vary in their rate of molecular evolution? Biology letters 5(3): 401–404.

Bromham, L., A. Rambaut, and P. H. Harvey. 1996. Determinants of rate variation in mammalian DNA sequence evolution. Journal of molecular evolution 43(6): 610–621.

Bürkner, P.-C. 2017. Bayesian distributional non-linear multilevel modeling with the r package brms. arXiv preprint arXiv:1705.11123.

Bürkner, P.-C., and E. Charpentier. 2020. Modelling monotonic effects of ordinal predictors in Bayesian regression models. British Journal of Mathematical and Statistical Psychology 73(3): 420–451.

Carling, G., and C. Cathcart. 2021. Reconstructing the evolution of Indo-European Grammar. Language 97: 1–38.

Carpenter, B., A. Gelman, M. D. Hoffman, D. Lee, B. Goodrich, M. Betancourt, M. Brubaker, J. Guo, P. Li, and A. Riddell. 2017. Stan: A probabilistic programming language. Journal of statistical software 76(1).

Cathcart, C., B. Herce, and B. Bickel. 2022. Decoupling speed of change and long-term preference in language evolution: Insights from Romance verb stem alternations. In The evolution of language: Proceedings of the Joint Conference on Language Evolution (JCoLE), Nijmegen, ed. by A. Ravignani, R. Asano, D. Valente, F. Ferretti, S. Hartmann, M. Hayashi, Y. Jadoul, M. Martins, Y. Oseki, E. D. Rodrigues, O. Vasileva, and S. Wacewicz, pp. 101–108. Joint Conference on Language Evolution (JCoLE).

Cathcart, C. A., A. Hölzl, G. Jäger, P. Widmer, and B. Bickel. 2020. Numeral classifiers and number marking in Indo-Iranian: A phylogenetic approach. Language Dynamics and Change 1(aop): 1–53.

Chang, W., C. Cathcart, D. Hall, and A. Garrett. 2015. Ancestry-constrained phylogenetic analysis supports the Indo-European Steppe Hypothesis. Language 91(1): 194–244.

Dediu, D. 2010. A Bayesian phylogenetic approach to estimating the stability of linguistic features and the genetic biasing of tone. Proceedings of the Royal Society of London B 278(1704): 474–79.

Dediu, D. 2021. Tone and genes: New cross-linguistic data and methods support the weak negative effect of the ”derived” allele of aspm on tone, but not of microcephalin. Plos one 16(6): e0253546.

Dediu, D., R. Janssen, and S. R. Moisik. 2017. Language is not isolated from its wider environment: vocal tract influences on the evolution of speech and language. Language & Communication 54: 9–20.

Dediu, D., S. R. Moisik, W. Baetsen, A. M. Bosman, and A. L. Waters-Rist. 2021. The vocal tract as a time machine: inferences about past speech and language from the anatomy of the speech organs. Philosophical Transactions of the Royal Society B 376(1824): 20200192.

Dixon, R. M. 1997. The rise and fall of languages. Cambridge University Press.

Dryer, M., and M. Haspelmath. 2013. World Atlas of Linguistic Structures. Leipzig: Max Planck Institute for Evolutionary Anthropology.

Duanmu, S. 2004. Tone and non-tone languages: An alternative to language typology and parameters. Language and Linguistics 5(4): 891–923.

Dunn, M., T. K. Dewey, C. Arnett, T. Eythórsson, and J. Barðdal. 2017. Dative sickness: A phylogenetic analysis of argument structure evolution in Germanic. Language 93(1): e1–e22.

Dunn, M., S. J. Greenhill, S. C. Levinson, and R. D. Gray. 2011. Evolved structure of language shows lineage-specific trends in word-order universals. Nature 473(7345): 79–82.

Esher, L. 2016, 3. Morphomes and predictability in the history of Romance perfects. Diachronica 32(4): 494–529.

Everett, C. 2013. Evidence for direct geographic influences on linguistic sounds: The case of ejectives. PloS one 8(6): e65275.

Everett, C. 2017. Languages in drier climates use fewer vowels. Frontiers in Psychology 8: 1285.

Everett, C., D. E. Blasi, and S. G. Roberts. 2015. Climate, vocal folds, and tonal languages: Connecting the physiological and geographic dots. Proceedings of the National Academy of Sciences 112(5): 1322–1327.

Felsenstein, J. 1981. Evolutionary trees from DNA sequences: A maximum likelihood approach. Journal of Molecular Evolution 17(6): 367–76.

Felsenstein, J. 2004. Inferring phylogenies. Sunderland, Mass.: Sinauer Associates.

Fitch, W. 1971. Rate of change of concomitantly variable codons. Journal of Molecular Evolution 1(1): 84–96.

Gabry, J., and R. Češnovar. 2021. cmdstanr: R Interface to ’CmdStan’. https://mc-stan.org/cmdstanr/; https://discourse.mc-stan.org.

Gill, M. S., L. S. Tung Ho, G. Baele, P. Lemey, and M. A. Suchard. 2017. A relaxed directional random walk model for phylogenetic trait evolution. Systematic biology 66(3): 299–319.

Goedemans, R., and H. van der Hulst. 2013a. Fixed stress locations. In The World Atlas of Language Structures Online, ed. by M. S. Dryer, and M. Haspelmath. Leipzig: Max Planck Institute for Evolutionary Anthropology.

Goedemans, R., and H. van der Hulst. 2013b. Weight-sensitive stress. In The World Atlas of Language Structures Online, ed. by M. S. Dryer, and M. Haspelmath Leipzig: Max Planck Institute for Evolutionary Anthropology.

Greenhill, S. J., X. Hua, C. F. Welsh, H. Schneemann, and L. Bromham. 2018. Population size and the rate of language evolution: a test across Indo-European, Austronesian, and Bantu languages. Frontiers in psychology 9: 576.

Greenhill, S. J., C.-H. Wu, X. Hua, M. Dunn, S. C. Levinson, and R. D. Gray. 2017. Evolutionary dynamics of language systems. Proceedings of the National Academy of Sciences 114(42): E8822–E8829.

Haynie, H. J. 2014. Geography and spatial analysis in historical linguistics. Language and Linguistics Compass 8(8): 344–357.

Haynie, H. J., and C. Bowern. 2016. Phylogenetic approach to the evolution of color term systems. Proceedings of the National Academy of Sciences 113(48): 13666–13671.

Heath, T., M. Holder, and J. Huelsenbeck. 2011. A Dirichlet Process Prior for estimating lineage-specific substitution rates. Molecular biology and evolution 29: 939–55.

Heggarty, P., A. Shimelman, G. Abete, C. Anderson, S. Sadowsky, L. Paschen, W. Maguire, L. Jocz, M. J. Aninao, L. Wägerle, D. Dërmaku-Appelganz, A. P. d. C. e. Silva, L. C. Lawyer, J. Michalsky, A. S. A. C. Cabral, M. Walworth, E. Koile, J. Runge, and H.-J. Bibiko. 2019. Sound Comparisons: Exploring Diversity in Phonetics across Language Families. Proceedings of the 19th International Congress of Phonetic Sciences, Melbourne, Australia 2019 ed. by S. Cahoun, P. Escudero, M. Tabain, and P. Warren.

Herce, B. 2019. Morphome interactions. Morphology 29(1).

Höhna, S., M. J. Landis, T. A. Heath, B. Boussau, N. Lartillot, B. R. Moore, J. P. Huelsenbeck, and F. Ronquist. 2016. RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Systematic Biology 65(4): 726–736.

Horvilleur, B., and N. Lartillot. 2014. Monte Carlo algorithms for Brownian phylogenetic models. Bioinformatics 30(21): 3020–3028.

Huebner, S. R. 2020. Climate change in the breadbasket of the Roman empire: Explaining the decline of the Fayum villages in the third century CE. Studies in Late Antiquity 4(4): 486–518.

Huelsenbeck, J. P., and M. A. Suchard. 2007. A nonparametric method for accommodating and testing across-site rate variation. Systematic Biology 56(6): 975–987.

Hyman, L. M. 2006. Word-prosodic typology. Phonology 23(2): 225–257.

Irvahn, J., and V. N. Minin. 2014. Phylogenetic stochastic mapping without matrix exponentiation. Journal of Computational Biology 21(9): 676–690.

Jäger, G. 2018. Global-scale phylogenetic linguistic inference from lexical resources. Scientific Reports 5.

Jäger, G. and J. Wahle. 2021. Phylogenetic typology. Frontiers in Psychology 12.

Jing, Y., M. Norvik, O. Vesakoski, and M. Dunn. 2022. Phylogenetic multilevel models reveal a simplicity bias in Uralic. In The evolution of language: Proceedings of the Joint Conference on Language Evolution (JCoLE), Nijmegen, ed. by A. Ravignani, R. Asano, D. Valente, F. Ferretti, S. Hartmann, M. Hayashi, Y. Jadoul, M. Martins, Y. Oseki, E. D. Rodrigues, O. Vasileva, and S. Wacewicz, pp. 357–360. Joint Conference on Language Evolution (JCoLE).

Koile, E., S. J. Greenhill, D. E. Blasi, R. Bouckaert, and R. D. Gray. 2022. Phylogeographic analysis of the Bantu language expansion supports a rainforest route. Proceedings of the National Academy of Sciences 119(32): e2112853119.

Lartillot, N. 2013. Phylogenetic patterns of GC-biased gene conversion in placental mammals and the evolutionary dynamics of recombination landscapes. Molecular biology and evolution 30(3): 489–502.

Lartillot, N., and R. Poujol. 2011. A phylogenetic model for investigating correlated evolution of substitution rates and continuous phenotypic characters. Molecular biology and evolution 28(1): 729–744.

Lemey, P., A. Rambaut, J. J. Welch, and M. A. Suchard. 2010. Phylogeography takes a relaxed random walk in continuous space and time. Molecular Biology and Evolution 27(8): 1877–1885.

Lopez, P., D. Casane, and H. Philippe. 2002. Heterotachy, an important process of protein evolution. Molecular biology and evolution 19(1): 1–7.

Maddieson, I. 2018. Language adapts to environment: Sonority and temperature. Frontiers in Communication 3: 28.

Maiden, M. 2018. The Romance verb: Morphomic structure and diachrony. Oxford University Press.

Maiden, M., J. C. Smith, S. Cruschina, M.-O. Hinzelin, and M. Goldbach. 2010. Oxford Online Database of Romance Verb Morphology. University of Oxford. Online at http://romverb-morph.clp.ox.ac.uk/.

McWhorter, J. 2007. Language interrupted: Signs of non-native acquisition in standard language grammars. Oxford: Oxford University Press.

Meade, A., and M. Pagel. 2008. A phylogenetic mixture model for heterotachy. In Evolutionary biology from concept to application, pp. 29–41. Springer.

Moisik, S. R., and D. Dediu. 2017. Anatomical biasing and clicks: Evidence from biomechanical modeling. Journal of Language Evolution 2(1): 37–51.

Nettle, D. 1999. Is the rate of linguistic change constant? Lingua 108(2-3): 119–136.

Neureiter, N., P. Ranacher, R. van Gijn, B. Bickel, and R. Weibel. 2021. Can Bayesian phylogeography reconstruct migrations and expansions in linguistic evolution? Royal Society open science 8(1): 201079.

Nichols, J., and C. Bentz. 2019. Morphological complexity of languages reflects the settlement history of the Americas. New Perspectives on the Peopling of the Americas, ed. by K. Harvati, G. Jäger, and H. Reyes-Centeno, pp. 13–26. Tübingen: Kerns Verlag.

O’Meara, B. C., C. Ané, M. J. Sanderson, and P. C. Wainwright. 2006. Testing for different rates of continuous trait evolution using likelihood. Evolution 60(5): 922–933.

Pagel, M. 1994. Detecting correlated evolution on phylogenies: A general method for the comparative analysis of discrete characters. Proceedings of the Royal Society of London B 255: 37–45.

Pagel, M., Q. D. Atkinson, and A. Meade. 2007. Frequency of word-use predicts rates of lexical evolution throughout Indo-European history. Nature 449: 717–720.

Pagel, M., and A. Meade. 2006. Bayesian analysis of correlated evolution of discrete characters by Reversible-Jump Markov Chain Monte Carlo. The American Naturalist 167(6): 808–25.

Pagel, M., and A. Meade. 2008. Modelling heterotachy in phylogenetic inference by reversible-jump Markov chain Monte Carlo. Phil. Trans. R. Soc. B 363: 3955–3964.

Penney, J. et al. 2011. Archaic and Old Latin. In A companion to the Latin language, ed. by J. Clackson, pp. 220–235. Blackwell.

Pronk, T. 2018. Language contact and prosodic change in Slavic and Baltic. Diachronica 35(4): 552–580.

Rasmussen, C. E., and C. K. I. Williams. 2006. Gaussian Processes for Machine Learning. Cambridge, MA: MIT Press.

Rice, K. 2014. Convergence of prominence systems. In Word Stress: Theoretical and Typological Issues, ed. by H. van der Hulst, pp. 194–227. Cambridge: Cambridge University Press Cambridge.

Ringen, E., J. S. Martin, and A. Jaeggi. 2021. Novel phylogenetic methods reveal that resource-use intensification drives the evolution of “complex” societies. EcoEvoRxiv.

Riutort-Mayol, G., P.-C. Bürkner, M. R. Andersen, A. Solin, and A. Vehtari. 2020. Practical Hilbert space approximate Bayesian Gaussian processes for probabilistic programming. arXiv preprint arXiv:2004.11408.

Roberts, S. G. 2018. Robust, causal, and incremental approaches to investigating linguistic adaptation. Frontiers in psychology 9: 166.

Shirtz, S., L. Talamo, and A. Verkerk. 2021. The evolutionary dynamics of negative existentials in Indo-European. Front. Commun. 6: 661862. doi: 10.3389/fcomm.

Stan Development Team. 2019. RStan: the R interface to Stan. R package version 2.19.2.

Tavaré, S. 1986. Some probabilistic and statistical problems in the analysis of DNA sequences. Lectures on Mathematics in the Life Sciences 17(2): 57–86.

Trudgill, P. 2001. Contact and simplification: Historical baggage and directionality in linguistic change. Linguistic Typology 5(2/3): 371–374.

Tuffley, C. and M. Steel. 1998. Modeling the covarion hypothesis of nucleotide substitution. Mathematical Biosciences 147(1): 63–91.

Urban, M. 2020. Mountain linguistics. Language and Linguistics Compass 14(9): e12393.

Urban, M., and S. Moran. 2021. Altitude and the distributional typology of language structure: Ejectives and beyond. Plos one 16(2): e0245522.

Vehtari, A., J. Gabry, M. Magnusson, Y. Yao, P.-C. Bürkner, T. Paananen, and A. Gelman. 2020. loo: Efficient leave-one-out cross-validation and WAIC for Bayesian models. R package version 2.4.1.

Vehtari, A., A. Gelman, and J. Gabry. 2017. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and computing 27(5): 1413–1432.

Wang, H.-C., M. Spencer, E. Susko, and A. J. Roger. 2007. Testing for covarion-like evolution in protein sequences. Molecular biology and evolution 24(1): 294–305.

Wichmann, S., E. W. Holman, and C. H. Brown. 2018. The ASJP database (version 18). http://asjp.clld.org/.

Wilson, F. M., P. A. Pappas, and A. O. Mooers. 2019. The role of frequency of use in lexical change: Evidence from Latin and Greek. Diachronica 36(4): 584–612.

Yao, Y., A. Vehtari, D. Simpson, and A. Gelman. 2017. Using stacking to average Bayesian predictive distributions. Bayesian Analysis.

(please see PDF for appendix)