Abstract
The identification of close relatives is central to forensic sciences and to genetic association studies, in which spurious signals can be obtained if genetic structure is not taken into account. Identifying related individuals is also essential in archaeological studies to elucidate funerary practices, as well as to obtain a deeper understanding of past family structures and social behaviors in the absence of written records. In the past decade, following the advent of high-throughput DNA sequencing, many statistical methods have been developed to calculate kinship coefficients from genome-wide data. However, these methods are inappropriate when DNA is sequenced at insufficient depth-of-coverage, presenting high levels of post-mortem damage, as is commonly observed with ancient molecules. These methods also generally require the presence of a reference panel, which cannot be accessed in the vast majority of paleogenomic studies. Here, I review the different approaches available for inferring relatedness, focusing on those compatible with the idiosyncrasies of ancient genomic data. I then present some of the key studies taking advantage of these analytical tools, ranging from simple sample curation to addressing long-standing archaeological debates on the emergence of the nuclear family and on the role of biological kinship in past societies.
Introduction: Why is relatedness inference important?
Many genetic tests have become commercially available in the last decade, especially for those interested in their genealogical history and/or deeper ancestry. For less than a hundred dollars and a saliva sample, ancestry genetic testing companies provide their customers with relatedness estimates, compared against the data of whomever agreed to share genotyping information. Despite their success on a global scale, genetic ancestry kits have also raised legitimate concerns on ethics and data protection (Kennett et al. 2018).
Reliable methods for relatedness inference were developed for applications in a number of scientific fields. For example, in forensics, they are part of routine paternity testing, as well as for victim identification in cases where confident attribution of fragmentary remains to a single individual is not possible (Brenner and Weir 2003; Fernandes et al. 2017). In population genetics and genome-wide association studies, related individuals are identified in populations and cohorts and excluded from analyses since they do not represent statistically independent samples. In medical genetics, the presence of closely related individuals in association studies inflates rates of false positives; therefore, relatedness among individuals must always be tested beforehand. In practice, screening human panels for cryptic relatedness has become a routine quality control, as it is not rare that datasets contain unreported familial relationships as close as first degree (e.g., siblings), or even data from identical individuals (Stevens et al. 2011). Beyond medical genetics, inferring relatedness is crucial to the conservation of endangered species, as mating between closely related individuals leads to inbreeding. Finally, deciphering the genetic relatedness between individuals is key for understanding past human societies, as this information could provide major insights into social structures, traditions, cultures and behavior. For example, it has often been suggested that kindred played an important role in structuring past societies, but only the combination of archaeological evidence and genetic proof of biological relatedness can confirm this hypothesis.
In this chapter, I will summarize the different methods that are available today and make use of genome-wide sequence data to infer relatedness, with a focus on those tailored to ancient DNA data (Part I). I will then illustrate the wide range of applications that these methods have in archaeological science (Part II). The two parts may be read independently, depending on the readers’ own interests.
Part I: Different methods for different data
In the following, I survey the different methods available to infer kinship between past individuals, starting from the simple amplification by Polymerase Chain Reaction (PCR) of uniparental markers, to the most elaborate statistical processing of whole genome data. This part of the chapter will review the basics of pedigrees and kinship coefficients. It will also dive a bit deeper into the caveats of ancient DNA data, such as the low amount of available DNA molecules and the lack of contemporaneous reference panels, as well as the potential presence of population structure or the possibly high levels of inbreeding, which make it necessary to choose between alternative statistical methods that can account for these specificities.
Relatedness inference using genetic markers: Mitochondrial and Y-haplogroups, autosomal STR
Until recently, past potential kinship was mainly assessed through two types of uniparental markers: mitochondrial DNA and the non-recombining region of the Y chromosome. Despite its major impact in first-generation ancient DNA studies (Gerstenberger et al. 1999; Rogaev et al. 2009), as well as in forensic science with the example of paternity testing, this approach faces crucial pitfalls. Mitochondrial DNA is present in numerous copies per cell (which facilitates lab work), is maternally inherited and helps retrace maternal lineages. The Y-chromosome is paternally inherited, thus providing evolutionary and genealogical information on paternal lineages. Restricting the analyses to unilineal markers has two major consequences. First, as most of the mitochondrial and Y-chromosome haplotypes are widely distributed in populations, they can only be used reliably to exclude close relatedness, such as father-son and mother-offspring relationships from Y-chromosome and mitochondrial DNA data, respectively. Second, the Y chromosome only provides information on the unique lineage composed exclusively of the father at each generation and cannot elucidate father-daughter relationships. Reciprocally, mitochondrial DNA is only informative about maternal lineages. Looking back 10 generations ago in the genealogy of a given individual, those uniparental markers would give access to the genetic background of only two ancestors, and not the more than one thousand that in fact existed (in theory 210=1,024, assuming unrelated ancestors). This contrasts to autosomal data, which can provide information transmitted by a larger number of ancestors (although not all).
As the quantity and quality of DNA samples available to forensic and ancient DNA laboratories may be very similar, any methodological development implemented in one field can benefit the other. For example, the gold standard for paternity testing in criminal or mass murder victim identification has been, from the 1990s onwards, the use of Short Tandem Repeats (STR), also known as microsatellites. In this approach, selected loci spread across the Y chromosome (or the autosomes), are amplified through PCR, and genotyped for the number of short motif repeats they carry. As these STR loci are multiallelic, characterizing only a few of them can help draw reliable conclusions on close familial relationships or consanguinity. For instance, the tests approved for paternity testing or offender identification are based on the amplification of 20 (US Combined DNA Index System) or 15 (Extended European Standard System Set) STR loci only. They show sufficient statistical power for elucidating parent-offspring relationships and the majority of sibling pairs, as well as for identifying historical characters. Famous examples are provided by the eight members of the House of Konigsfeld, Germany, spanning seven generations (1546-1749 AD, Gerstenberger 1999), or the last Russian Emperor Nicholas II, whose children have been identified and confirmed dead 91 years after they were murdered during the Russian Civil War (Rogaev et al. 2009).
Wider kinship, such as first cousins, cannot be reliably assessed on the basis of STR test profiles alone. In those cases, it becomes necessary to genotype a third individual who could be a closer relative to both individuals under investigation (Nothnagel et al. 2010). In addition, STRs have proven hard to genotype from degraded DNA extracted from ancient remains. Some of the targeted loci indeed span over more than 250 base pairs (bp, Gerstenberger et al. 1999), whereas the average fragment length for ancient DNA lies around 50 bp. Therefore, the success of STR amplification is generally very limited (Deguilloux et al. 2013) and, at best, only partial profiles can be obtained (Russo et al. 2016; Haak et al. 2008; Cui et al. 2015), which rules out this approach for most archaeological assemblages.
The development of molecular and bioinformatic tools tailored to ancient remains, as well as the rapidly growing High-Throughput Sequencing (HTS) technologies, made it possible to publish the first complete genome of a past human individual (Rasmussen et al. 2010). This major achievement opened the door to elucidating kinship between past humans not solely based on the isolated markers just mentioned, but on genome-scale data, even though genealogy and genetic relatedness are not synonymous, as described below.
From pedigree to relatedness inference, and back
The interest of the general public for commercial DNA testing (e.g., through the company 23andMe®, etc.) has enhanced the confusion between genealogy and genetic relatedness, and between genetic data and culture. We should emphasize that genealogy and genetic relatedness cannot be superimposed (Reich 2018). The genealogy of one individual, as can be redrawn from familial and historical records, groups together all their known ascendants. In contrast, as a result of the random nature of DNA recombination, the genome of some of our numerous genealogical ascendants certainly did not contribute to any of our DNA. As a consequence, even the most extensive and accurate whole-genome analysis would not be able to redraw some of the family links, simply because the descendant did not inherit any fraction of the genome of some of his/her distant ancestors.
If two individuals are genetically related, they will not only share a recent common ancestor, as genealogic relatives do, but they would also have co-inherited a portion from the genome of that ancestor. If we consider two individuals that are the Nth generation descendants of one given couple, they will share an allele identical-by-descent (IBD) if this allele has been copied and transmitted to the two descendants over 2N consecutive meiosis events. The probability of a copy to be transmitted over each generation equals 0.5 (1 chance over 2 chromosomes). Therefore the probability that the allele is inherited by each of the two Nth generation descendants under study is 21-2N. Following this, after only N=4 generations, the probability of the copy being inherited through both lineages appears less than 1% (~0.78%). When family trees (or pedigrees) are known, it is relatively straightforward to deduce the probability of any of the genotypes present in any pair of individuals. But the reciprocal is not true: finding the probability of an inferred relatedness knowing the genotypes, or sometimes even partial genotyping data or likelihood of genotypes, can be challenging. While it is not possible to track IBD alleles directly, one can instead leverage the observed genotypes to identify alleles identical-by-state (IBS). Those are used to obtain probabilities of the IBD status of the alleles, and then to make statistical inferences about the degree of relatedness. In the following chapter section, we will review the different coefficients expressing these degrees of relatedness, how they are calculated, and which conclusions can be drawn from their values.
How relatedness degrees and coefficients should be understood
Table 1 provides a summary of different familial relationships and their corresponding relatedness. The relatedness between two individuals can be represented by the shortest lineage path, or the number of parent-offspring steps, from one individual to the other. In the pedigree presented as an example in Figure 1A, L is the child of F, therefore the lineage path between them is one, over one single line of descent. In contrast, I and L are first cousins and can be linked by two lineage paths of length four, over two lines of descent (I-D-A-F-L and I-D-B-F-L).
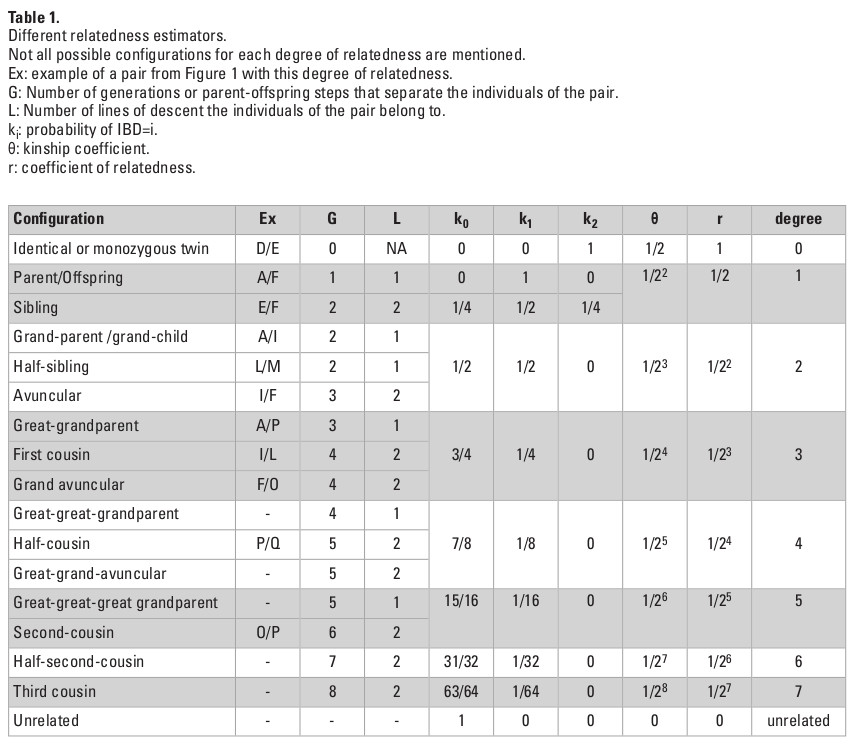
The kinship coefficient (θ) quantifies the number of generation steps that separate the individuals of the pair and formalizes the relatedness between two individuals. In the pedigree presented in Figure 1A, I and L have both A and B as most recent common ancestors. Their kinship coefficient can be expressed as:
θ(I,L)=(1+fA)/2gA+1 + (1+fB)/2gB+1
where gX represents the number of parent-offspring steps between I and L via X (X standing for either A or B in our case). fX is the inbreeding coefficient of X, corresponding in fact to the kinship coefficient of his/her parents. In our case, gA=gB=4. Assuming that A and B are unrelated (fA=fB=0), we obtain the following:
θ(I,L)=2x(1/25)=1/16 (i.e., 6.25%).
An allele from individual I has one in 16 chances of being descended from the same parental allele as an allele from L. In the eventuality of I and L being inbred, for instance if A and B were first cousins (θ(A,B)=1/16), we would have obtained a higher value of θ:
θ(I,L)= 2x((1+0,0625)/25)=17/256 (i.e., 6.64%).
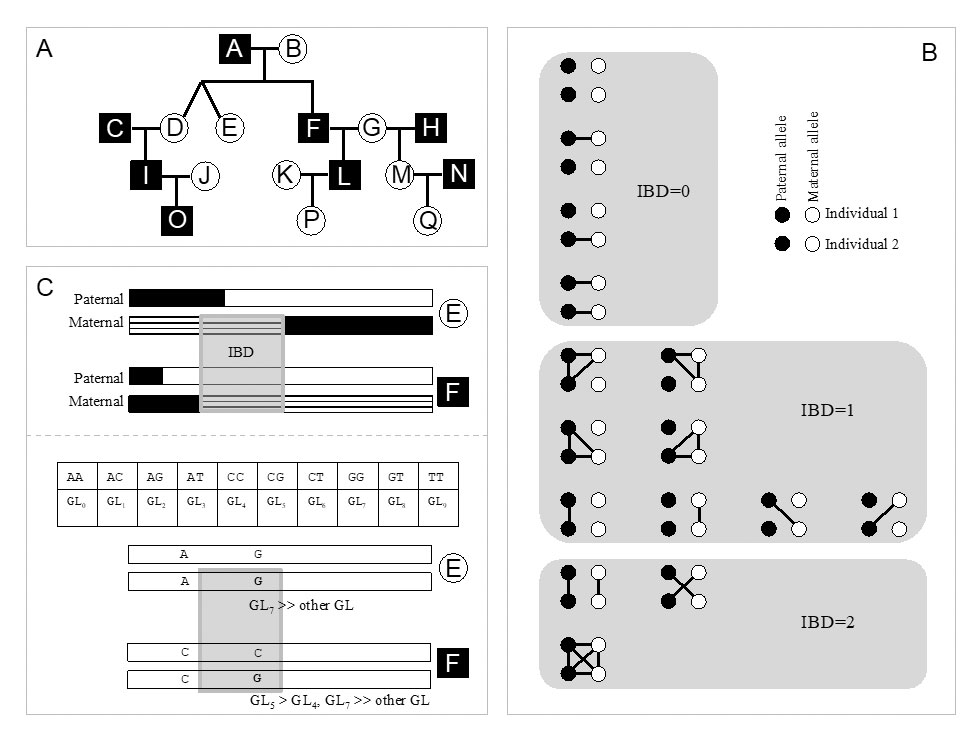
In the context of ancient individuals, the pedigree is most likely to be unknown, and the calculations above can not be applied. A kinship coefficient is first calculated based on genomic data, and the most probable degree of relatedness between individuals is then deduced from this coefficient. The kinship coefficient θ can be defined as the probability that a randomly chosen allele in an individual is IBD to a randomly selected homologous allele in the second individual. For a pair of diploid individuals, there are 15 possible IBD states (Fig. 1B). It is generally not possible (but also not necessary in many cases) to distinguish between maternal or paternal alleles. Therefore, the possible different IBD sharing patterns for any given locus are condensed into nine and their probabilities are called Jacquard coefficients (Jacquard 1974). The frequencies of each of these nine distinct patterns estimate the common ancestry between the two individuals and their inbreeding level. When neither individual is expected to show significant level of inbreeding, IBD states can be further reduced to three (IBD=0, IBD=1 or IBD=2), with probabilities of IBD=0, IBD=1 and IBD=2 referred to as k0, k1 and k2, respectively. In the case of no inbreeding (which is assumed in the majority of studies), θ can be expressed as follows:
θ = k1/4+k2/2.
In practice, IBD-segment based methods calculate k1 and k2 as the cumulative genetic length of the IBD=1 and IBD=2 segments, respectively, divided by the total genetic length of the genome. Relying solely on the probability that a random allele from one individual is IBD to the random allele of another makes it impossible to distinguish between a number of possible cases within the same degree. For example, the θ coefficient between sibling pairs and parents and their offspring is equal to 50%. However, the pattern of allele sharing is different. In this case, characterizing the set of IBD sharing coefficients (k0, k1 and k2) is necessary to solve the true degree of relatedness (Table 1). It is noteworthy that even though k0, k1 and k2 coefficients specify the expected fraction of genome sharing between two relatives, the actual sharing measured might strongly differ from these expected values as a result of the random nature of recombination. For instance, the expected IBD sharing between siblings is 50%, while the 95% confidence interval lies between 37 and 63% (Speed and Balding 2015), with variance around the expected 50% value being greater for sibling pairs than for parent-offspring. Other deviations may be introduced by the choice of sequencing technology or relatedness estimators.
Using the power of genomics to infer kinship between ancient individuals
It is now possible to measure genome sharing directly from genome-wide single-nucleotide polymorphism data (SNP), obtained either from HTS DNA sequencing of shotgun or captured libraries (or directly from SNP microarray genotyping when sufficient amounts of fresh DNA are available). To estimate the frequencies of IBD sharing patterns, different approaches have been developed (Table 2). They are either based on the method of moments (Population-based LINKage analyses, PLINK, Purcell et al. 2007), which has the computational efficiency to exploit the potential of large data sets, or on maximum likelihood estimations (Kinship-base INference for Genome-wide association studies, KING, Manichaikul et al. 2010).
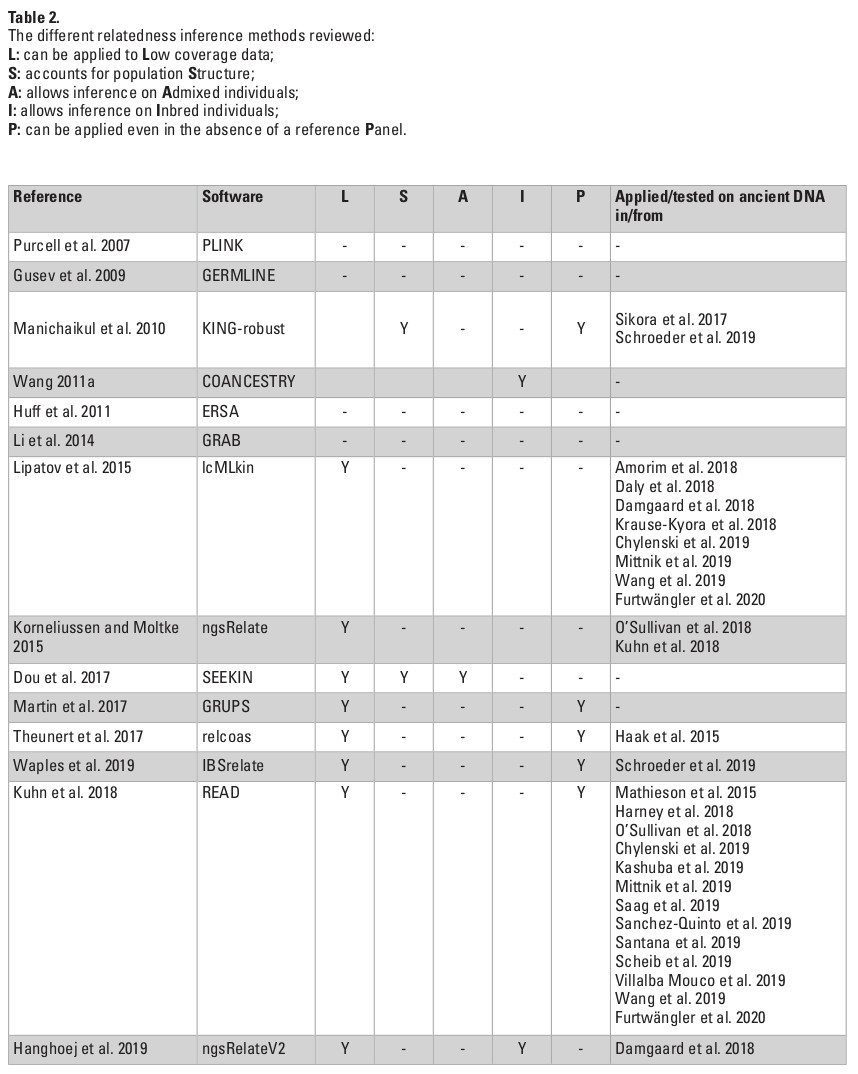
In these methods, genetic relatedness is quantified through the calculation of allele-sharing coefficients (Manichaikul et al. 2010), which rely on identifying putative IBD regions from expanding seeds of matching genotypes between individuals (GERMLINE, Genetic Error-tolerant Regional Matching with LInear-time Extension, Gusev et al. 2009). Alternatively, genetic relatedness is calculated on the basis of pre-defined IBD segments (ERSA, Estimation of Recent Shared Ancestry, Huff et al. 2011). These methods can be highly accurate in detecting distant relatedness up to the 13th degree (ERSA, Huff et al. 2011), but their quality requirements make them difficult, if not impossible, to apply to ancient DNA data.
Indeed, for the very vast majority of archaeological samples, no pedigrees are known, and no reference panels providing reliable past allele frequencies in the population are available. In addition, only low-coverage data are generally accessible, and include significant amounts of errors due to post-mortem damage and, in some cases, contamination introduced by one or more present-day individuals. Furthermore, many algorithms assume that the individuals are from the same homogeneous population, without substructure or admixture, and show no significant level of inbreeding. The nature of ancient DNA data, thus, requires the implementation of dedicated statistical methods. These methodologies are developed further below, and account for the specificities of ancient genome-wide data, namely their low coverage, the absence of a contemporaneous reference panel, and the potential occurrence of admixture, population structure, or inbreeding.
Dealing with sparse DNA sequencing data
DNA extracts obtained from ancient remains consist of a mixture of endogenous molecules from the individual of interest, and contaminant molecules deriving from the environment, the laboratory reagents and the scientists handling the remains (e.g., archaeologists and/or the geneticists). The discovery that ancient DNA preservation was maximized in petrous bones or tooth cementum, and the development of molecular approaches tailor-made to the biochemical nature of ancient molecules have been instrumental in improving the quality of ancient DNA datasets (Orlando et al. 2015). Nevertheless, high coverage genomic data can rarely be obtained at a reasonable cost, and the vast majority of ancient human genomes are limited to low coverage data.
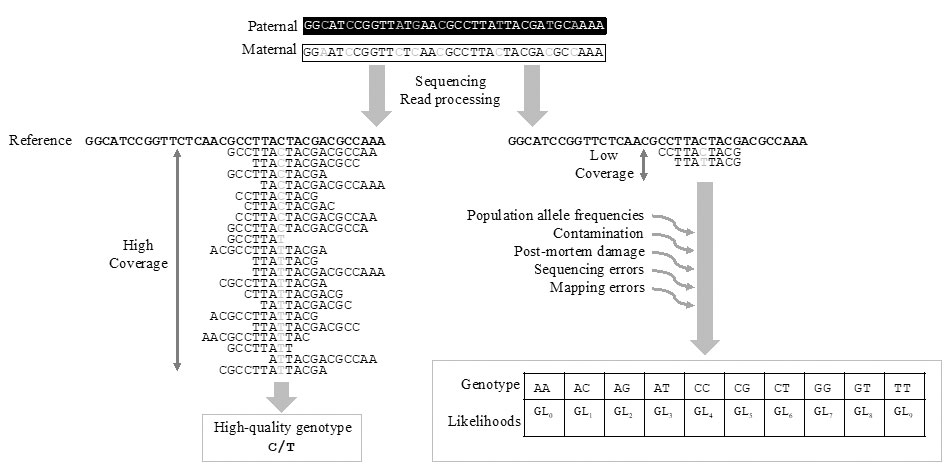
Unfortunately, computational methods adapted to vast modern cohorts, such as PLINK (Purcell et al. 2007), GERMLINE (Gusev et al. 2009) and KING (Manichaikul et al. 2010), require inputs in the form of high-quality genotype data (Fig. 2) and can therefore not be directly applied to the low-depth HTS data obtained from the majority of ancient human remains. Indeed, when the genome is sequenced to low-depth (<5X coverage), there is a high probability that only one of the two alleles has been sampled at a specific site, making accurate genotype calling difficult, if not impossible. Such sparse data may lead to an underestimation of the true level of heterozygosity (Renaud et al. 2018). Therefore, when applied to called genotypes from low coverage data, software tools like PLINK (Purcell et al. 2007) tend to overestimate the fraction of IBD=0 (k0) and as a consequence underestimate relatedness.
To mitigate the uncertainty when calling genotypes from low-depth HTS data, dedicated programs which incorporate uncertainty of the genotypes in maximum likelihood estimates of pairwise relatedness have been developed (NgsRelate, Korneliussen 2015; lcMLkin, Lipatov et al. 2015). These methods are not based on genotypes, but on genotype likelihoods instead, i.e., on the probability of the observed data in the sequencing read given the true genotype. They thereby take into account the uncertainty of the genotype, described by a quality score or a genotype likelihood that incorporates errors introduced, for instance, by postmortem damage during sequencing or while mapping to the reference genome (Fig. 2). Of note, these algorithms require similar levels of uncertainty across samples. Applying them to different batches of samples showing different qualities, for instance samples sequenced using different platforms, can bias relatedness estimates. Moreover, they can only be applied to medium-to-low coverage data (2-4X) and not to extremely-low coverage data, unlike other methods based on genetic distances (Martin et al. 2017).
SNP-based methods also require a set of shared SNPs to be covered in all the genomes compared, which can be limiting in low-coverage sequencing contexts. To overcome this, SEEKIN (SEquence-based Estimation of KINship; Dou et al. 2017) leverages the correlation between neighboring markers. Even if the number of common SNPs sequenced in two individuals assessed for relatedness is low, Linkage Disequilibrium (LD) neighboring SNPs can be exploited to call genotypes over SNPs that were not directly sequenced. This results in a significant increase in the total number of SNP positions shared.
One example of successful characterization of family links from extremely low depth sequencing is the identification, 100 years after his death, of the remains of an Irish rebel buried in a shallow grave, which was made possible by the comparison with genetic data from living relatives (Fernandes et al. 2017). The depth of coverage obtained after shotgun sequencing was as low as 0.04X for the deceased, and 0.08-0.1X for presumed second-degree relatives. Since very few SNPs were covered by more than one sequencing read, a forced homozygous approach served as the basis for estimating kinship coefficients (Queller and Goodnight 1989) using the European allele frequencies estimated by “The 1000 Genomes Project” (The 1000 Genomes Project Consortium 2015). Such an approach is efficient in terms of sequencing budget, computing time and accuracy, but can be applicable only in the few cases in which several known close relatives can be included, and when the ancient individual is recent enough that a modern reference panel can be used to assess allelic frequencies. How to proceed when this is not the case, in other words when no proper reference panel can be used to obtain reliable allele frequencies in the population, is the subject of the following chapter section.
How to proceed when no reference panels are available?
Many methods rely on the availability of accurate genotype frequencies from the focal population. Present-day populations can be used as a reference panel only for recent historical individuals (Fernandes et al. 2017). Applying this strategy to more ancient individuals can result in highly-overestimated genetic relatedness, e.g., supporting unrealistic values for individuals living several thousands of years apart (Sikora et al. 2017).
This limitation is not specific to genome-wide SNPs but also applies to STR-based estimations in forensics, where the population to which a suspect belongs is most often unknown (Caliebe and Krawczak 2018), or in genetics applied to historical or archaeological samples (Cui et al. 2015; Russo et al. 2016). For instance, funerary practices in the territory of Argentina before Hispanic contact was estimated based on previously published STR data from other pre-Hispanic populations from Peru (Baca et al. 2012), but also, as these data were not sufficient to serve as a reference panel on their own, from contemporary populations (Russo et al. 2016).
Methods that do not necessitate a reference panel still require at least a pair of unrelated individuals from the same population for normalization (READ, Relationship Estimation from Ancient DNA, Kuhn et al. 2018), or genomic data from several other ancient individuals of the same population (Martin et al. 2017; Theunert et al. 2017). The smaller the number of individuals available, the less accurate the kinship coefficient, regardless of the number of genomic sites considered. For example, simulation studies show that with as few as 18 individuals, the method developed by Theunert and colleagues cannot identify second-degree relatives (Theunert et al. 2017). In addition, approaches like READ (Kuhn et al. 2018) are sensitive to batch effects (shotgun versus capture, or data obtained with different sequencing platforms), which can overestimate the genetic distance indicative of unrelated individuals and, thus, the degree of relatedness in the tested samples.
Without access to data from an unrelated pair of the same population, only very few methods can be applied to very small datasets, for comparing a single pair of individuals or to establish relatedness within a single pedigree. KING, for example, is a robust algorithm that can infer relatedness up to the third degree based on information from only two individuals analyzed, but only when high-density genotyping data are available (Manichaikul et al. 2010).
How to proceed in the presence of admixture and population structure?
As mentioned earlier, most algorithms used to estimate relatedness assume that the individuals analyzed belong to a genetically homogeneous population (Purcell et al. 2007; Milligan 2003; Albrechtsen et al. 2009). In the case of admixture, the individuals show different ancestry backgrounds, which violates this assumption. In the case of population structure, the relatedness between individuals belonging to the same subpopulation will be systematically inflated. As a consequence, many approaches face circularity: while the identification of unrelated individuals is a prerequisite to the detection of population structure (Zhu et al. 2008), proper relatedness inference relies on the identification of homogeneous populations (Purcell et al. 2007).
Several methods have been developed to overcome this limitation and provide kinship estimation for admixed individuals (Wang 2011b; Relatedness Estimation in Admixed Populations, REAP, Thornton et al. 2012; and RelateAdmix, Moltke and Albrechtsen 2014, also providing admixture proportions). To account for the different ancestry backgrounds in admixed individuals, these approaches use allele frequencies specific to each individual derived from software like ADMIXTURE (Alexander et al. 2009). The KING-robust estimator (Manichaikul et al. 2010) is designed to deal with population structure, but shows lower performance when analyzing admixed individuals (Thornton et al. 2012). However, the estimators mentioned above require accurate genotype data, which may not be available in the majority of paleogenomic studies thus far. The SEEKIN estimator (Dou et al. 2017) can infer kinship for both homogeneous and heterogeneous samples with population structure and admixture. It was initially designed to improve kinship estimation in target-enrichment experiments by incorporating off-target reads (0.15X average depth), but can be advantageously applied to shallow sequencing data.
Inbreeding
All the relatedness estimators reviewed so far in this chapter indicate that the individuals investigated are not inbred. However, in archaeological contexts, suspicions that this is not the case are worth considering. For example, past hunter-gatherers were previously found to present a high level of skeletal abnormalities, which was interpreted as the consequence of inbreeding among small human groups (Trinkaus et al. 2014). High inbreeding levels were not, however, confirmed by ancient DNA data (Sikora et al. 2017). Can small amounts of inbreeding affect kinship estimates? How shall we treat data from dynasties with a known history of consanguinity?
At the genomic level, inbreeding results in an excess of homozygosity compared to what would be expected under Hardy-Weinberg Equilibrium, which describes the relationship between allele frequencies and genotype frequencies in a randomly mating population (see Andrews 2010 for a review of the basics). In this case, estimating only k0, k1 and k2 is insufficient, and the nine condensed Jacquard coefficients have to be determined (see section ‘How should relatedness degrees and coefficients be understood’). Some methods like COANCESTRY (Wang 2011a) have been developed to estimate relatedness in the presence of inbreeding, but they cannot be applied to low coverage data as they are based on high quality genotypes. At present, ngsRelate v2 (Hanghøj et al. 2019) is the only software based on genotype likelihoods that can infer relatedness in the presence of inbreeding while providing inbreeding coefficients for both individuals considered.
Paleogenomicists now have at hand a whole suite of software enabling them to exploit the power of genomic data in order to assess how much two past individuals were in fact related from a biological point of view. In the following , I present some of the key studies leveraging these tools to facilitate sample curation and for helping solve longstanding archaeological disputes.
Part II: Applications
This section will review the major recent publications making use of the statistical methods for kinship inferences between ancient individuals that we detailed in Part I. It will cover a wide range of applications, from data curation by collapsing sample duplicates or removing related individuals from the dataset prior to population genetics studies, to questioning the definition of a ‘family’ in the archaeological past and elucidating some aspects of social structure in past societies.
Relatedness inferences as a tool for sample and data curation
One of the very first and most straightforward applications of relatedness inference on ancient remains was to reveal unidentified duplicated samples (Table 3). The fragmentation and dispersion of bones found in collective burials and domestic waste, or of remains stored in bulk for many years in museum collections, make it difficult to certify that each and every fragment analyzed is from a different individual. Restricting the analyses to petrous bones from the same side of the skull (Daly et al. 2018) or to teeth in connection to the mandible can limit spurious resampling, but is not always an option. After shallow shotgun sequencing or targeted enrichment, systematic processing of relatedness estimation between pairs of samples has revealed kinship coefficients indicative of monozygous twins, most likely representing independent remains from the same individual (Daly et al. 2018; Villalba-Mouco et al. 2019; Wang et al. 2019; Theunert et al. 2017 reanalyzing data from Haak et al. 2015). In the majority of cases, data from both samples can simply be collapsed into one single individual, but in a few others, they should be discarded (Daly et al. 2018 data coming from petrous bones of the same side). Moreover, testing for potential relatedness may be useful if artifacts were produced by the same individual. Indeed, birch bark mastics, commonly used from the Middle Paleolithic onwards as chewing gum but also as an adhesive in lithic tool technology, can fossilize teeth or finger imprints and very surprisingly were also identified as ancient DNA reservoirs, opening the possibility of a direct connection between genetics and a material culture (Kashuba et al. 2019). For example, low-coverage genomes (0.1 to 0.5X) could be reconstructed from three of these pre-historic mastics, excavated in the Mesolithic site of Huseby Klev, Sweden (Kashuba et al. 2019). By performing kinship analyses between these samples, the authors could confirm each of them was processed by a different individual, but the low coverages obtained, combined with the very limited number of samples and the absence of a reference panel, prevented any conclusions to be drawn on their relatedness.
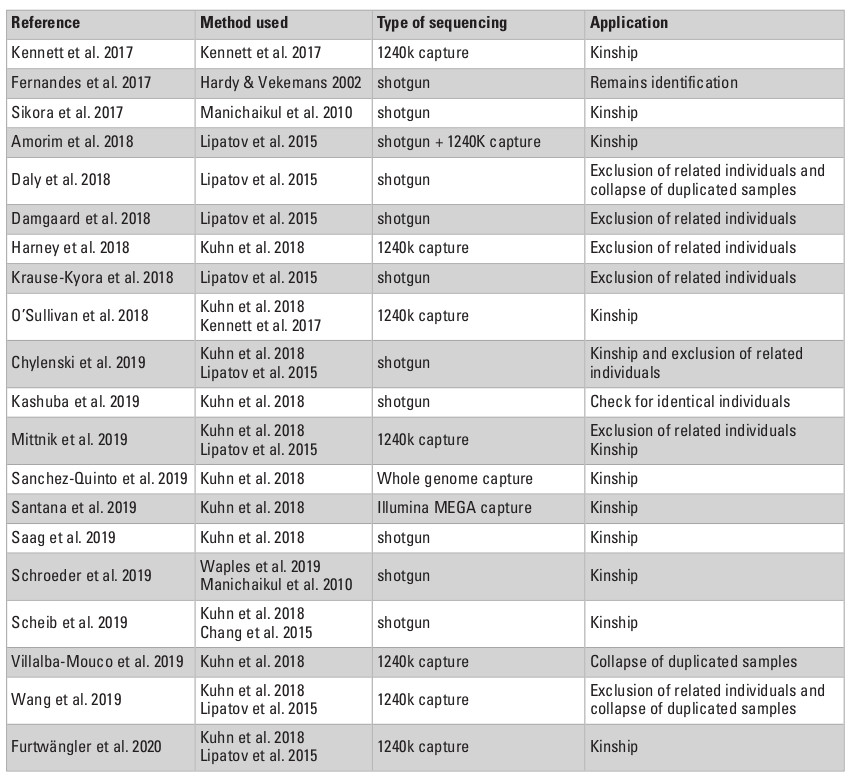
Kinship coefficients can also be used to test for the presence of potential cross-contamination between samples processed during the same experimental sessions, which would bear relatedness across different sites and/or time periods (Villalba-Mouco et al. 2019). Identifying first or second-degree parents in an ancient panel is also crucial, as including those may bias population frequencies-based statistics. When present, relatives with the lower coverage are filtered out of assessments on population genetics (Damgaard et al. 2018; Daly et al. 2018; Harney et al. 2018; Chylenski et al. 2019; Wang et al. 2019). Similarly, testing for the absence of related individuals is necessary before validating their inclusion into a panel for identifying a susceptibility locus to certain diseases (e.g., leprosy, Krause-Kyora et al. 2018).
The emergence of the nuclear family as the basis of social relationships
In present-day societies, biological relatedness is the foundation for many of our social interactions, including heritage, marriage rules, parental authority, support obligation, etc. When did this start? Was genetic kinship such a key driver of social organization in the past?
Determining the genetic kinship of past individuals buried together or in a close proximity provides important insights into the social organization in (pre-)historic cultures. To infer potential familial links, and ultimately reconstruct pedigrees or lineages, measures of relatedness obtained from genomic data provides one good starting point. It should, however, always be combined with stratigraphic information, radiocarbon dates, the age and the sex of the individual, etc. This multi-proxy approach was applied on the individuals buried at Sunghir (Russia), which is dated to ~35,000 years BP, and hosts two of the most extraordinary Upper Paleolithic burials known to date (Sikora et al. 2017). In a first pit, an adult male, Sunghir 1, was buried together with thousands of beads made of mammoth ivory, most likely sewn on his clothes. In the other burial, two juvenile individuals, Sunghir 2 and Sunghir 3, were interred head-to-head. They were also both covered in approximately 10,000 beads, but these were slightly smaller as if they were scaled to the height of the children. Among the breath-taking grave goods excavated, we can cite a belt made of almost 300 pierced fox canines, as well as a dozen ivory spears, including one that was 2.5 m long. Surprisingly, a human femoral diaphysis from a fourth individual was found next to Sunghir 2; it was broken, polished and filled with ochre. The Sunghir site represents one of the exceptional cases of multiple individuals buried simultaneously, or originating from very close temporal and spatial proximity. These individuals may thus represent a single social group and provide unprecedented information on the behavior and kinship structure in an Upper Paleolithic society. Based on the artifacts and anatomical observations, the three individuals were often interpreted as members of the same nuclear family: Sunghir 1 as the father of a son (Sunghir 2) and a daughter (Sunghir 3) (Trinkhaus et al. 2014). Genome analyses told a different story, first revealing all four individuals as males (Sikora et al. 2017). All four individuals also carried the same mitochondrial genome sub-haplogroup U2 (in accordance with a West Eurasian and Siberian Paleolithic background) and the same Y-chromosome haplogroup C1a2. Despite this, and the anatomical similarities observed, none of the Sunghir individuals were found to be closely related, at least not up to the third degree, as indicated by a method that does not rely on unknown allele frequencies for Upper Paleolithic populations (Manichaikul et al. 2010).
Inbreeding was also examined for Sunghir 3, as the skeletal pathologies that his remains displayed were previously interpreted as evidence for elevated inbreeding. The cumulative length of long Run Of Homozygosity (ROH), used as a proxy for inbreeding, was found to be higher than in most ancient genomes, but shorter than in archaic and modern populations with a known history of isolation and consanguinity (Sikora et al. 2017). This rules out recent inbreeding in Sunghir individuals despite small population size, which indicates that groups of restricted size and limited kinship were embedded in a larger mating network, similar to what is observed in present-day hunter-gatherers. Even though the debate about active and conscious avoidance of consanguinity is still open, the Sunghir genomes support the existence of regular exchanges of mates between groups, which is also consistent with archaeological evidence of high mobility in the Upper Paleolithic, and may have impacted the development of knowledge transfer between bands.
The earliest molecular identification of a nuclear family (mother-father-child) dates back to ~ 30,000 years later. Schroeder and colleagues (Schroeder et al. 2019) have performed a systematic analysis of the genomes of 15 late Neolithic individuals buried in a mass grave at Koszyce, in today’s Southern Poland (2,880-2,776 BCE). As in Sikora et al. 2017, the authors used a method based on pairwise sharing of alleles IBS (see section ‘From pedigree to relatedness inference, and back’), similar to the one formalized by Waples and colleagues (Waples et al. 2019) and combined with kinship estimators (KING, Manichaikul et al. 2010). This combination allowed the authors not only to discriminate among the different first three degrees of relatedness, but also, within first degree related pairs, to identify parent-offspring or full-siblings (Table 1). Relatedness inferences showed that individuals were positioned in the grave according to kindred relations, highlighting that social and biological relationships could, at least to some extent, be superimposed, and confirming that family relations were key to the community organization. In particular, according to the arrangement of the deceased within the pit, maternal kinship and brotherhood were considered as an important form of social investment, important enough to be perpetuated in death. This mass murder situation is also an exceptional case where several individuals were buried simultaneously and immediately after their death, making the hypothesis of corpse repatriation very unlikely: obviously, people were buried in the exact place where they lived just before their death. Of note, even though results are consistent with the community being organized along patrilineal lines of descent, women in different family positions (mothers, daughters, sisters) are present in the burial. Interestingly, both daughters identified were sub-adults (13-14 and 15-16 years old), whereas four of the seven identified sons were already adults (and a fifth at 16-17 years old). Therefore, these observations are consistent with the hypothesis of patrilocality, where women leave their parents and find a partner in another location while men stay, or at least come back as adults, to the community where they were born.
In a more recent study, including 13 sites dated from the Late Neolithic to the Bronze Age and located in Switzerland, South Germany and French Alsace, 27 of 96 individuals whose genome-wide data have been analyzed were identified using lcMLkin (Lipatov et al. 2015) and READ (Kuhn et al. 2018) to be related at the first or second degree, within nine familial groups (Furtwängler et al. 2020). This result underlies the importance of kinship in these societies. Strikingly, the vast majority of these related individuals were males (22/27) and all but one of the females were mothers of one or two identified sons, adding some arguments to the hypothesis of patrilocality and social importance of the male lineage.
Both case studies above (Schroeder et al. 2019; Furtwängler et al. 2020) identified full brother/sisterhoods are largely predominant in numbers over half-sisterhoods, and the only half-brothers identified have the same father (but a different mother). This observation, which can only be accessed through genetic relatedness inference, is key for understanding the nature of a family nucleus during the Late Neolithic and Bronze Age in Germany and Switzerland, with most likely a stable parental couple between a local male and a non-local female, and possibly polygamy or re-union for men. In the next section, further examples provide information on unilineal descent groups, as well as the correlation between these mating rules and social stratification.
Complex societies and unilineal descent groups
There is a long-standing debate, in anthropology and in the social sciences in general, about the importance of kinship and unilineal (matrilineal or patrilineal) descent groups in modeling the structure, hierarchy and evolution of complex societies. What are the rules underlying the choice of high-ranking members of a given community? Do biological factors, such as kinship or age, dominate social rank? Or is leadership, which is based on life-time achievements such as success at war or hunting, more important? Inferring relatedness among members of a burial that could be defined as an elite burial through its architecture, context, grave goods or personal adornments can help address the hypothesis of potentially institutionalized heredity of leadership in pre-historic societies. Finding a link between the presence of related individuals and rich grave goods can indicate that material wealth or elite status was transferred from parent to offspring.
Pueblo Benito, New Mexico, was both the spiritual and political center of the Chacoan society, one of North America’s earliest complex societies (Chaco Canyon, 800 CE-1,130 CE). By analyzing genome-wide capture data from individuals interred in one of its most elaborate elite burials, Kennett and colleagues revealed a community organized as a matrilineal dynasty (Kennett et al. 2017). They calculated relatedness coefficients with an approach similar to the one formalized by Kuhn and colleagues (Kuhn et al. 2018). Here, genomes were pseudohaploidized following random sampling of an allele. The average mismatch rate across all autosomal SNPs was then computed and normalized by the highest mismatch rate observed among all the individuals, assuming that the corresponding specific pair of individuals belonged to the same population and were unrelated. This is the first study of its kind that confirmed the importance of genetic kindred in highly complex and structured societies.
In contrast, studies investigating past European societies revealed social organization based around male lines of descents. For example, this was true for the Lombards, who ruled over part of Italy for over 200 years and took part in the migrations that shaped European societies during the 4th-6th century CE. As written records about these migrations are highly partial and settlements barely known, questions about their identity and social organization could only be addressed through funerary archaeology and ancient DNA. Two Lombard cemeteries, located in Hungary and Northern Italy, were sampled and screened for DNA preservation (Amorim et al. 2018). A total of 55 individuals provided sufficient genome-wide capture data to be scanned for relatedness using lcMLkin (Lipatov et al. 2015). As reference allele frequencies, the authors used those of the ancient individuals themselves combined with those from the present-day 1000 Genome populations. In addition, they adapted the lcMLkin software to incorporate admixture and to account for diverse genetic ancestry. This study highlighted the fact that groups interred in both cemeteries appeared to be organized around one extended male kindred of high status, according to their level of meat consumption and the associated artifacts and grave goods. This conclusion underlined that biological relatedness may have played a major role in the structure and hierarchy of these societies.
A recent study on individuals excavated from a 7th century CE Alemanni site in southern Germany reminds us that social structure involves more subtle factors than single, linear familial transmission of culture and power. Here, the burials delivered extremely rich grave goods, including jewelry, equestrian gear, and weapons, demonstrating the wealth and power of the household, and suggesting contacts with Byzantines, Lombards and Franks. Genome-wide SNP enrichment could be performed on a selection of eight male individuals (O’Sullivan et al. 2018) and kinship was estimated based on the proportion of non-matching autosomal genotypes (Kennett et al. 2017; Kuhn et al. 2018). Five individuals, coming from five different graves, including two multiple burials, and accompanied by culturally different artifacts, appeared as first and second-degree relatives. This surprising result underlines that burial patterns and assignment of grave goods do not necessarily reflect genetic relatedness. It also highlights that cultural appropriation from diverse origins can be found even among relatives as close as father and son. On the other hand, the presence of non-relatives within the same grave suggests that social fellowship could be held equally as with biological relatedness in this Alemanni funerary site. This confirms analyses of historical records indicating that, in the Merovingian period, being part of a household was not limited to biological relatives.
As described earlier, such patrilineal social organization in western Europe seems to extend back at least to the late Neolithic (Schroeder et al. 2019; Furtwängler et al. 2020). Mittnik and colleagues have recently performed an archaeo-genomic study integrating genome-wide capture data, material culture, as well as strontium and oxygen stable isotope analyses of 104 individuals from the Lech Valley, Germany, spanning from the Late Neolithic to the Middle Bronze Age (Mittnik et al. 2019). They discuss the hypothesis that households were, at that time and region, socially stratified institutions. Indeed, in the vicinity of farmsteads, three different types of burials were identified: those associated with rich grave goods and holding the remains of members of the same family; those well-furnished but where non-local adult women were buried; and a third burial type with low-status, unrelated women. Interestingly, among the 10 different parent-offspring relations identified, the offspring was systematically a male (adult in 9 out of 10 cases), indicating that daughters may have had to leave their parental home. This observation is consistent with isotopic and archaeological evidence suggesting that high-status women identified on site were from non-local origin, most likely coming from several hundreds of kilometers away. Of note, these studies (Schroeder et al. 2019; Mittnik et al. 2019; Furtwängler et al. 2020) focus only on Central Europe (Poland, Germany, Switzerland). Considerable extra sampling and sequencing efforts are still needed before their conclusions can be used to generalize on a wider European scale.
Conclusion
A wide range of methods and software tools have been designed for inferring relatedness from genomic or genome-wide SNP data. A total of 12 methods have been benchmarked, showing high accuracy for first- and second-degree relationships in modern DNA data (Ramstetter et al. 2017). IBD-based methods, however, appeared more accurate and more efficient in deciphering distant relatedness than methods relying on independent markers. The idiosyncrasies of ancient DNA data, such as the absence of reference panels, the diverse molecular tools or platforms used, the uncertainty on strict sample contemporaneity, or the various coverage achieved across individuals, preclude similar benchmarking on real data. The power and accuracy of relatedness inference methods can, however, be evaluated through simulations (Martin et al. 2017; Hanghøj et al. 2019) or on small sample size datasets (Theunert et al. 2017). Methods developed for shallow genome sequencing can not only benefit forensics and ancient DNA studies, but also be applied to wild animal survey through non-invasive sample collections (e.g., fecal baboon DNA, Snyder-Mackler et al. 2016), off-target regions in target sequencing studies (Dou et al. 2017), or very large sample size studies where only very low coverage sequencing is affordable. The best strategy remains debatable, especially as combining the inferences from different methods does not seem to drastically enhance the accuracy of the relatedness inferences drawn (Ramstetter et al. 2017). Future approaches may not be restricted to pairwise comparisons, but instead will also exploit the relatedness signals obtained from multiple individuals.
Applied to ancient humans, these molecular analyses aim at serving as tools to complement historical and archaeological approaches in order to get a deeper understanding of past societies. For many years, major paleogenomic studies have been based on sampling individuals across multiple sites, assumed to be representative of a defined culture (Haak et al. 2015; Allentoft et al. 2015; Olalde et al. 2018). Some of the most recent studies favor a micro-regional approach and attempt to characterize the genomes of all possible individuals in a multiple/collective burial or in a cemetery, aiming at revealing its entire genomic complexity. In combination with the study of material culture, funerary practices, isotopic data, physical anthropology, paleopathology and others, molecular approaches to kinship inference will help us better understand the rules and factors underpinning the organization of past societies.
Acknowledgements
The author is grateful to Clio Der Sarkissian, Antoine Fages and Ludovic Orlando for their critical reading of the manuscript. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 795916.
References
Albrechtsen, A., T. S. Korneliussen, I. Moltke, T. van Overseem Hansen, F. C. Nielsen, and R. Nielsen. 2009. Relatedness mapping and tracts of relatedness for genome-wide data in the presence of linkage disequilibrium. Genetic Epidemiology 33: 266–274.
Alexander, D. H., J. Novembre, and K. Lange. 2009. Fast model-based estimation of ancestry in unrelated individuals. Genome Research 19: 1655–1664.
Allentoft, M. E., M. Sikora, K.-G. Sjogren, S. Rasmussen, M. Rasmussen, J. Stenderup, P. B. Damgaard, H. Schroeder, T. Ahlstrom, L. Vinner, A.-S. Malaspinas, A. Margaryan, T. Higham, D. Chivall, N. Lynnerup, L. Harvig, J. Baron, P. Della Casa, P. Dabrowski, P. R. Duffy, A. V. Ebel, A. Epimakhov, K. Frei, M. Furmanek, T. Gralak, A. Gromov, S. Gronkiewicz, G. Grupe, T. Hajdu, R. Jarysz, V. Khartanovich, A. Khokhlov,V. Kiss, J. Kolar, A. Kriiska, I. Lasak, C. Longhi, G. McGlynn, A. Merkevicius,I. Merkyte, M. Metspalu, R. Mkrtchyan, V. Moiseyev, L. Paja, G. Palfi, D. Pokutta, Ł Pospieszny, T. D. Price, L. Saag, M. Sablin, N. Shishlina,V. Smrcka, V. I. Soenov,V Szeverenyi, G Toth, S. V. Trifanova, L. Varul, M. Vicze, L. Yepiskoposyan, V. Zhitenev, L. Orlando, T. Sicheritz-Ponten, S. Brunak, R. Nielsen, K. Kristiansen and E. Willerslev. 2015. Population genomics of Bronze Age Eurasia. Nature 522: 167–172.
Amorim, C. E. G., S. Vai, C. Posth, A. Modi, I. Koncz, S. Hakenbeck, M. C. La Rocca, B. Mende, D. Bobo, W. Pohl, L. Pejrani Baricco, E. Bedini, P. Francalacci, C. Giostra, T. Vida, D. Winger, U. von Freeden, S. Ghirotto, M. Lari, G. Barbujani, J. Krause, D. Caramelli, P. J. Geary, and K. R. Veeramah. 2018. Understanding 6th-century barbarian social organization and migration through paleogenomics. Nature Communications 9: 3547.
Andrews, C. 2010. The Hardy-Weinberg Principle. Nature Education Knowledge 3 (10): 65.
Baca, M., K. Doan, M. Sobczyk, A. Stankovic, and P. Węgleński.2012. Ancient DNA reveals kinship burial patterns of a pre-Columbian Andean community. BMC Genetics 13: 30.
Brenner, C. H. and B.S. Weir. 2003. Issues and strategies in the DNA identification of World Trade Center victims. Theoretical Population Biology 63: 173–178.
Caliebe, A., and M. Krawczak. 2018. Match probabilities for Y-chromosomal profiles: A paradigm shift. Forensic Science International: Genetics 37: 200–203.
Chang, C. C., C. C. Chow, L. C. Tellier, S. Vattikuti, S. M. Purcell, and J. J. Lee. 2015. Second-generation PLINK: Rising to the challenge of larger and richer datasets. Gigascience 4: 7.
Chylenski, M., E. Ehler, M. Somel, R. Yaka, M. Krzewinska, M. Dabert, A. Juras, and A. Marciniak. 2019. Ancient mitochondrial genomes reveal the absence of maternal kinship in the burials of Çatalhöyük people and their genetic affinities. Genes 10: 3390.
Cui, Y., L. Song, D. Wei, Y. Pang, N. Wang, C. Ning, C. Li, B. Feng, W. Tang, H. Li, Y. Ren, C. Zhang, Y. Huang, Y. Hu, and H. Zhou. 2015. Identification of kinship and occupant status in Mongolian noble burials of the Yuan Dynasty through a multidisciplinary approach. Philosophical Transactions of the Royal Society B 370: 20130378.
Daly, K. G., P. M. Delser, V. E. Mullin, A. Scheu, V. Mattiangeli, M. D. Teasdale, A. J. Hare, J. Burger, M. P. Verdugo, M. J. Collins, R. Kehati, C. M. Erek, G. Bar-Oz, F. Pompanon, T. Cumer, C. Çakırlar, A. F. Mohaseb, D. Decruyenaere, H. Davoudi, Ö. Çevik, G. Rollefson, J.-D. Vigne, R. Khazaeli, H. Fathi, S. B. Doost, R. R. Sorkhani, A. A. Vahdati, E. W. Sauer, H. A. Kharanaghi, S. Maziar, B. Gasparian, R. Pinhasi, L. Martin, D. Orton, B. S. Arbuckle, N. Benecke, A. Manica, L. K. Horwitz, M. Mashkour, and D. G. Bradley. 2018. Ancient goat genomes reveal mosaic domestication in the Fertile Crescent. Science 361: 85–88.
Damgaard, P. d. B., R. Martiniano, J. Kamm, J. V. Moreno-Mayar, G. Kroonen, M. Peyrot, G. Barjamovic, S. Rasmussen, C. Zacho, N. Baimukhanov, V. Zaibert, V. Merz, A. Biddanda, I. Merz, V. Loman, V. Evdokimov, E. Usmanova, B. Hemphill, A. Seguin-Orlando, F. E. Yediay, I. Ullah, K.-G. Sjögren, K. H. Iversen, J. Choin, C. de la Fuente, M. Ilardo, H. Schroeder, V. Moiseyev, A. Gromov, A. Polyakov, S. Omura, S. Y. Senyurt, H. Ahmad, C. McKenzie, A. Margaryan, A. Hameed, A. Samad, N. Gul, Muhammad Hassan Khokhar25, O. I. Goriunova, V. I. Bazaliiskii, J. Novembre, A. W. Weber, L. Orlando, M. E. Allentoft, R. Nielsen, K. Kristiansen, M. Sikora, A. K. Outram, R. Durbin, and E. Willerslev. 2018. The first horse herders and the impact of early Bronze Age steppe expansions into Asia. Science 360: eaar7711.
Deguilloux, M. F., M. H. Pemonge, F. Mendisco, D. Thibon, I. Cartron, and D. Castex. 2013. Ancient DNA and kinship analysis of human remains deposited in Merovingian necropolis sarcophagi (Jau Dignac et Loirac, France, 7th-8th century AD). Journal of Archaeological Science 41: 399–405.
Dou, J., B. Sun, X. Sim, J. D. Hughes, D. F. Reilly, E. S. Tai, J. Liu, and C. Wang. 2017. Estimation of kinship coefficient in structured and admixed populations using sparse sequencing data. PLoS Genetics 13: e1007021.
Fernandes, D., K. Sirak, M. Novak, J. A. Finarelli, J. Byrne, E. Connolly, J. E. L. Carlsson, E. Ferretti , R. Pinhasi, and J. Carlsson. 2017. The identification of a 1916 Irish rebel: New approach for estimating relatedness from low coverage homozygous genomes. Scientific Reports 7: 41529.
Furtwängler, A., A. B. Rohrlach, T. C. Lamnidis, L. Papac, G. U. Neumann, I. Siebke, E. Reiter, N. Steuri, J. Hald, A. Denaire, B. Schnitzler, J. Wahl, M. Ramstein, V. J. Schuenemann, P. W. Stockhammer, A. Hafner, S. Lösch, W. Haak, S. Schiffels, and J. Krause. 2020. Ancient genomes reveal social and genetic structure of Late Neolithic Switzerland. Nature Communications 11: 1915.
Gerstenberger, J., S. Hummel, T. Schultes, B. Hack, and B. Herrmann. 1999. Reconstruction of a historical genealogy by means of STR analysis and Y-haplotyping of ancient DNA. European Journal of Human Genetics 7: 469–477.
Gusev, A., J. K. Lowe, M. Stoffel, M. J. Daly, D. Altshuler, J. L. Breslow, J. M. Friedman, and I. Pe’er. 2009. Whole population, genome-wide mapping of hidden relatedness. Genome Research 19: 318–326.
Haak, W., G. Brandt, H. N. de Jong, C. Meyer, R. Ganslmeier, V. Heyd, C. Hawkesworth, A. W. G. Pike, H. Meller, and K. W. Alt. 2008. Ancient DNA, Strontium isotopes, and osteological analyses shed light on social and kinship organization of the Later Stone Age. PNAS 105: 18226–18231.
Haak, W., I. Lazaridis, N. Patterson, N. Rohland, S. Mallick, B. Llamas, G. Brandt, S. Nordenfelt, E. Harney, K. Stewardson, Q. Fu, A. Mittnik, E. Banffy, C. Economou, M. Francken, S. Friederich, R. Garrido Pena, F. Hallgren, V. Khartanovich, A. Khokhlov, M. Kunst, P. Kuznetsov, H. Meller, O. Mochalov, V. Moiseyev, N. Nicklisch, S. L. Pichler, R. Risch, M. A. Rojo Guerra, C. Roth, A. Szecsenyi-Nagy, J. Wahl, M. Meyer, J. Krause, D. Brown, D. Anthony, A. Cooper, K. Werner Alt, and D. Reich. 2015. Massive migration from the steppe was a source for Indo-European languages in Europe. Nature 522: 207–211.
Han, L., and M. Abney. 2011. Identity by descent estimation with dense genome-wide genotype data. Genetic Epidemiology 35: 557–567.
Hanghøj, K., I. Moltke, P. A. Andersen, A. Manica and T. S. Korneliussen. 2019. Fast and accurate relatedness estimation from high-throughput sequencing data in the presence of inbreeding. GigaScience 8: 1–9.
Hardy, O. J., and X. Vekemans. 2002. Spagedi: A versatile computer program to analyse spatial genetic structure at the individual or population levels. Molecular Ecology Notes 2: 618–620.
Harney, E., H. May, D. Shalem, N. Rohland, S. Mallick, I. Lazaridis, R. Sarig, K. Stewardson, S. Nordenfelt, N. Patterson, I. Hershkovitz, and D. Reich. 2018. Ancient DNA from Chalcolithic Israel reveals the role of population mixture in cultural transformation. Nature Communications 9: 3336.
Huff, C. D., D. J. Witherspoon, T. S. Simonson, J. Xing, W. S. Watkins, Y. Zhang, T. M. Tuohy, D. W. Neklason, R. W. Burt, S. L. Guthery, S. R. Woodward, and L. B. Jorde. 2011. Maximum-likelihood estimation of recent shared ancestry (ERSA). Genome Research 21: 768–774.
Jacquard, A. 1974. The Genetic Structure of Populations. Biomathematics. Vol. 5. Berlin: Springer.
Kashuba, N., E. Kırdök, H. Damlien, M. A. Manninen, B. Nordqvist, P. Persson and A. Götherström. 2019. Ancient DNA from mastics solidifies connection between material culture and genetics of mesolithic hunter-gatherers in Scandinavia. Communications Biology 2: 185.
Kennett, D. J., S. Plog, R. J. George, B. J. Culleton, A. S. Watson, P. Skoglund, N. Rohland, S. Mallick, K. Stewardson, L. Kistler, S. A. LeBlanc, P. M. Whiteley, D. Reich, and G. H. Perry. 2017. Archaeogenomic evidence reveals prehistoric matrilineal dynasty. Nature Communications 8: 14115.
Kennett, D. A., A. Timpson, D. J. Balding, and M. G. Thomas. 2018. The rise and fall of Britains DNA: A tale of misleading claims, media manipulation and threats to academic freedom. Geneaolgy 2: 47.
Knipper, C., A. Mittnik, K. Massy, C. Kociumaka, I. Kucukkalipci, M. Maus, F. Wittenborn, S. E. Metz, A. Staskiewicz, J. Krause, and P. W. Stockhammer. 2017. Female exogamy and gene pool diversification at the transition from the Final Neolithic to the Early Bronze Age in central Europe. PNAS 114: 10083–10088.
Korneliussen, T. S., and I. Moltke. 2015. NgsRelate: A software tool for estimating pairwise relatedness from next-generation sequencing data. Bioinformatics 31: 4009–4011.
Krause-Kyora, B., M. Nutsua, L. Boehme, F. Pierini, D. D. Pedersen, S.-C. Kornell, D. Drichel, M. Bonazzi, L. Möbus, P. Tarp, J. Susat, E. Bosse, B. Willburger, A. H. Schmidt, J. Sauter, A. Franke, M. Wittig, A. Caliebe, M. Nothnagel, S. Schreiber, J. L. Boldsen, T. L. Lenz, and A. Nebel. 2018. Ancient DNA study reveals HLA susceptibility locus for leprosy in medieval Europeans. Nature Communications 9: 1569.
Kuhn, J. M. M., M. Jakobsson, and T. Gunther. 2018. Estimating genetic kin relationships in prehistoric populations. PLoS ONE 13: e0195491.
Li, H., G. Glusman, C. Huff, J. Caballero, and J. C. Roach. 2014. Accurate and robust prediction of genetic relationship from whole-genome sequences. PLoS ONE 9: e85437.
Lipatov, M., K. Sanjeevy, R. Patroy, and K. R. Veeramah. 2015. Maximum likelihood estimation of biological relatedness from low coverage sequencing data. bioRxiv. Cold Spring Harbor Labs Journals doi:10.1101/023374.
Lynch, M., and K. Ritland. 1999. Estimation of pairwise relatedness with molecular markers. Genetics 152: 1753–1766.
Manichaikul, A., J. C. Mychaleckyj, S. S. Rich, K. Daly, M. Sale, and W.-M. Chen. 2010. Robust relationship inference in genome-wide association studies. Bioinformatics 26: 2867–2873.
Martin, M. D., F. Jay, S. Castellano, and M. Slatkin. 2017. Determination of genetic relatedness from low-coverage human genome sequences using pedigree simulations. Molecular Ecology 26: 4145–4157.
Mathieson, I., I. Lazaridis, N. Rohland, S. Mallick, N. Patterson, S. A. Roodenberg, E. Harney, K. Stewardson, D. Fernandes, M. Novak, K. Sirak, C. Gamba, E. R. Jones, B. Llamas, S. Dryomov, J. Pickrell, J. L. Arsuaga, J. M. Bermúdez de Castro, E. Carbonell, F. Gerritsen, A. Khokhlov, P. Kuznetsov, M. Lozano, H. Meller, O. Mochalov, V. Moiseyev, M. A. Rojo Guerra, J. Roodenberg, J. M. Vergès, J. Krause, A. Cooper, K. W. Alt, D. Brown, D. Anthony, C. Lalueza-Fox, W. Haak, R. Pinhasi, and D. Reich. 2015. Genome-wide patterns of selection in 230 ancient Eurasians. Nature 528: 499–503.
Milligan, B. G. 2003. Maximum-likelihood estimation of relatedness. Genetics 163: 1153–1167.
Mittnik, A., K. Massy, C. Knipper, F. Wittenborn, R. Friedrich, S. Pfrengle, M. Burri, N. Carlichi-Witjes, H. Deeg, A. Furtwängler, M. Harbeck, K. von Heyking, C. Kociumaka, I. Kucukkalipci, S. Lindauer, S. Metz, A. Staskiewicz, A. Thiel, J. Wahl, W. Haak, E. Pernicka, S. Schiffels, P. W. Stockhammer, and J. Krause. 2019. Kinship-based social inequality in Bronze Age Europe. Science 366: 731–734.
Moltke, I., and A. Albrechtsen. 2014. RelateAdmix: A software tool for estimating relatedness between admixed individuals. Bioinformatics 30: 1027–1028.
Nothnagel, M., J. Schmidtke, and M. Krawczak. 2010. Potentials and limits of pairwise kinship analysis using autosomal short tandem repeat loci. International Journal of Legal Medicine 124: 205–215.
Olalde, I., S. Brace, M. E. Allentoft, I. Armit, K. Kristiansen, T. Booth, N. Rohland, S. Mallick, A. Szécsényi-Nagy, A. Mittnik, E. Altena, M. Lipson, I. Lazaridis, T. K. Harper, N. Patterson, N. Broomandkhoshbacht, Y. Diekmann, Z. Faltyskova, D. Fernandes, M. Ferry, E. Harney, P. de Knijff, M. Michel, J. Oppenheimer, K. Stewardson, A. Barclay, K. W. Alt, C. Liesau, P. Ríos, C. Blasco, J. V. Miguel, R. M. García, A. A. Fernández, E. Bánffy, M. Bernabò-Brea, D. Billoin, C. Bonsall, L. Bonsall, T. Allen, L. Büster, S. Carver, L. C. Navarro, O. E. Craig, G. T. Cook, B. Cunliffe, A. Denaire, K. E. Dinwiddy, N. Dodwell, M. Ernée, C. Evans, M. Kuchařík, J. F. Farré, C. Fowler, M. Gazenbeek, R. G. Pena, M. Haber-Uriarte, E. Haduch, G. Hey, N. Jowett, T. Knowles, K. Massy, S. Pfrengle, P. Lefranc, O. Lemercier, A. Lefebvre, C. H. Martínez, V. G. Olmo, A. B. Ramírez, J. L. Maurandi, T. Majó, J. I. McKinley, K. McSweeney, B. G. Mende, A. Modi, G. Kulcsár, V. Kiss, A. Czene, R. Patay, A. Endrődi, K. Köhler, T. Hajdu, T. Szeniczey, J. Dani, Z. Bernert, M. Hoole, O. Cheronet, D. Keating, P. Velemínský, M. Dobeš, F. Candilio, F. Brown, R. F. Fernández, A. M. Herrero-Corral, S. Tusa, E. Carnieri, L. Lentini, A. Valenti, A. Zanini, C. Waddington, G. Delibes, E. Guerra-Doce, B. Neil, M. Brittain, M. Luke, R. Mortimer, J. Desideri, M. Besse, G. Brücken, M. Furmanek, A. Hałuszko, M. Mackiewicz, A. Rapiński, S. Leach, I. Soriano, K. T. Lillios, J. L. Cardoso, M. P. Pearson, P. Włodarczak, T. D. Price, P. Prieto, P. J. Rey, R. Risch, M. A. R. Guerra, A. Schmitt, J. Serralongue, A. M. Silva, V. Smrčka, L. Vergnaud, J. Zilhão, D. Caramelli, T. Higham, M. G. Thomas, D. J. Kennett, H. Fokkens, V. Heyd, A. Sheridan, K. G. Sjögren, P. W. Stockhammer, J. Krause, R. Pinhasi, W. Haak, I. Barnes, C. Lalueza-Fox, and D. Reich. 2018. The Beaker phenomenon and the genomic transformation of northwest Europe. Nature 555: 190–198.
Orlando, L., M. T. Gilbert, and E. Willerslev. 2015. Reconstructing ancient genomes and epigenomes. Nature Reviews Genetics 16: 395–408.
O’Sullivan, N., C. Posth, V. Coia, V. J. Schuenemann, T. D. Price, J. Wahl, R. Pinhasi, A. Zink, J. Krause, and F. Maixner. 2018. Ancient genome-wide analyses infer kinship structure in an Early Medieval Alemannic graveyard. Science Advances 4: eaao1262.
Purcell, S., B. Neale, K. Todd-Brown, L. Thomas, M. A. R. Ferreira, D. Bender, J. Maller, P. Sklar, P. I. W. de Bakker, M. J. Daly, and P. C. Sham. 2007. PLINK: A tool set for whole-genome association and population-based linkage analyses. American Journal of Human Genetics 81: 559–575.
Queller, D. C., and K. F. Goodnight. 1989. Estimating relatedness using genetic markers. Evolution 43: 258–275.
Ramstetter, M. D., T. D. Dyer, D. M. Lehman, J. E. Curran, R. Duggirala, J. Blangero, J. G. Mezey, and A. L. Williams. 2017. Benchmarking relatedness inference methods with genome-wide data from thousands of relatives. Genetics 207: 75–82.
Rasmussen, M., Y. Li, S. Lindgreen, J. S. Pedersen, A. Albrechtsen, I. Moltke, M. Metspalu, E. Metspalu, T. Kivisild, R. Gupta, M. Bertalan, K. Nielsen, M. T. Gilbert, Y. Wang, M. Raghavan, P. F. Campos, H. M. Kamp, A. S. Wilson, A. Gledhill, S. Tridico, M. Bunce, E. D. Lorenzen, J. Binladen, X. Guo, J. Zhao, X. Zhang, H. Zhang, Z. Li, M. Chen, L. Orlando, K. Kristiansen, M. Bak, N. Tommerup, C. Bendixen, T. L. Pierre, B. Grønnow, M. Meldgaard, C. Andreasen, S. A. Fedorova, L. P. Osipova, T. F. Higham, C. B. Ramsey, T. V. Hansen, F. C. Nielsen, M. H. Crawford, S. Brunak, T. Sicheritz-Pontén, R. Villems, R. Nielsen, A. Krogh, J. Wang, and E. Willerslev. 2010. Ancient human genome sequence of an extinct Palaeo-Eskimo. Nature 463: 757–762.
Reich, D. 2018. Who we are and how we got here. Oxford: Oxford University Press.
Renaud G., K. Hanghøj, T. S. Korneliussen, E. Willerslev, and L. Orlando. 2019. Joint estimates of heterozygosity and runs of homozygosity for modern and ancient samples. Genetics 212: 587–614.
Rogaev, E. I., A. P. Grigorenko, Y. K. Moliaka, G. Faskhutdinova, A. Goltsov, A. Lahti, C. Hildebrandt, E. L. W. Kittler, and I. Morozova. 2009. Genomic identification in the historical case of the Nicholas II royal family. PNAS 106: 5258–5263.
Russo, M. G., F. Mendisco, S. A. Avena, C. B. Dejean, and V. Seldes. 2016. Pre-Hispanic mortuary practices in Quebrada de Humahuaca (North-Western Argentina): Genetic relatedness among individuals buried in the same grave. Annals of Human Genetics 80: 210–220.
Saag, L., M. Laneman, L. Varul, M. Malve, H. Valk, M. A. Razzak, I. G. Shirobokov, V. I. Khartanovich, E. R. Mikhaylova, A. Kushniarevich, C. L. Scheib, A. Solnik, T. Reisberg, J. Parik, L. Saag, E. Metspalu, S. Rootsi, F. Montinaro, M. Remm, R. Mägi, E. D’Atanasio, E. R. Crema, D. Diez-del-Molino, M. G. Thomas, A. Kriiska, T. Kivisild, R. Villems, V. Lang, M. Metspalu, and K. Tambets. 2019. The arrival of Siberian ancestry connecting the Eastern Baltic to Uralic speakers further East. Current Biology 29: 1701–1711.
Sánchez-Quinto, F., H. Malmström, M. Fraser, L. Girdland-Flink, E. M. Svensson, L. G. Simões, R. George, N. Hollfelder, G. Burenhult, G. Noble, K. Britton, S. Talamo, N. Curtis, H. Brzobohata, R. Sumberova, A. Götherström, J. Storå, and M. Jakobsson. 2019. Megalithic tombs in western and northern Neolithic Europe were linked to a kindred society. PNAS 116: 9469–9474.
Santana, J., F. J. Rodríguez-Santos, M. D. Camalich-Massieu, D. Martín-Socas, and R. Fregel. 2019. Aggressive or funerary cannibalism? Skull-cup and human bone manipulation in Cueva de El Toro (Early Neolithic, southern Iberia). American Journal of Physical Anthropology 169: 31–54.
Scheib, C. L., R. Hui, E. D’Atanasio, A. W. Wohns, S. A. Inskip, A. Rose, C. Cessford, T. C. O’Connell, J. E. Robb, C. Evans, R. Patten, and T. Kivisild. 2019. East Anglian early Neolithic monument burial linked to contemporary Megaliths. Annals of Human Biology 46: 145-149.
Schroeder, H., A. Margaryan, M. Szmyt, B. Theulot, P. Włodarczak, S. Rasmussen, S. Gopalakrishnan, A. Szczepanek, T. Konopka, T. Z. T. Jensen, B. Witkowska, S. Wilk, M. M. Przybyła, Ł. Pospieszny, K.-G. Sjögren, Z. Belka, J. Olsen, K. Kristiansen, E. Willerslev, K. M. Frei, M. Sikora, N. N. Johannsen, and M. E. Allentoft. 2019. Unraveling ancestry, kinship, and violence in a Late Neolithic mass grave. PNAS 116: 10705–10710.
Sikora, M., A. Seguin-Orlando, V. C. Sousa, A. Albrechtsen, T. Korneliussen, A. Ko, S. Rasmussen, I. Dupanloup, P. R. Nigst, M. D. Bosch, G. Renaud, M. E. Allentoft, A. Margaryan, S. V. Vasilyev, E. V. Veselovskaya, S. B. Borutskaya, T. Deviese, D. Comeskey, T. Higham, A. Manica, R. Foley, D. J. Meltzer, R. Nielsen, L. Excoffier, M. M. Lahr, L. Orlando, and E. Willerslev. 2017. Ancient genomes show social and reproductive behavior of early Upper Paleolithic foragers. Science 358: 659–662. doi: 10.1126/science.aao1807
Snyder-Mackler, N., W. H. Majoros, M. L. Yuan, A. O. Shaver, J. B. Gordon, G. H. Kopp, S. A. Schlebusch, J. D. Wall, S. C. Alberts, S. Mukherjee, X. Zhou, and J. Tung. 2016. Efficient genome-wide sequencing and low-coverage pedigree analysis from noninvasively collected samples. Genetics 203: 699–714.
Speed, D., and D. J. Balding. 2015. Relatedness in the post-genomic era: Is it still useful? Nature Reviews Genetics 16: 33–44.
Stevens, E. L., G. Heckenberg, E. D. O. Roberson, J. D. Baugher, T. J. Downey, and J. Pevsner. 2011. Inference of relationships in population data using identity-by-descent and identity-by-state. PLoS Genetics 7: e1002287. The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526: 68–74.
Theunert, C., F. Racimo, and M. Slatkin. 2017. Joint estimation of relatedness coefficients and allele frequencies from ancient samples. Genetics 206: 1025–1035.
Thornton, T., H. Tang, T. J. Hoffmann, H. M. Ochs-Balcom, B. J. Caan, and N. Risch. 2012. Estimating kinship in admixed populations. American Journal of Human Genetics 91: 122–138.
Trinkaus, E., A. P. Buzhilova, M. B. Mednikova, and M. V. Dobrovolskaya. 2014. The people of Sunghir. New York: Oxford University Press.
Villalba-Mouco, V., M. S. van de Loosdrecht, C. Posth, R. Mora, J. Martínez-Moreno, M. Rojo-Guerra, D. C. Salazar-García, J. I. Royo-Guillén, M. Kunst, H. Rougier, I. Crevecoeur, H. Arcusa-Magallón, C. Tejedor-Rodríguez, I. García-Martínez de Lagrán, R. Garrido-Pena, K. W. Alt, C. Jeong, S. Schiffels, P. Utrilla, J. Krause,and W. Haak. 2019. Survival of Late Pleistocene hunter-gatherer ancestry in the Iberian Peninsula. Current Biology 29: 1169–1177.
Wang, J. 2011a. COANCESTRY: A program for simulating, estimating and analysing relatedness and inbreeding coefficients. Molecular Ecology Resources 11: 141–5.
Wang, J. 2011b. Unbiased relatedness estimation in structured populations. Genetics 187: 887–901.
Wang, J. 2014. Marker-based estimates of relatedness and inbreeding coefficients: An assessment of current methods. Journal of Evolutionary Biology 27: 518–530.
Wang, C.-C., S. Reinhold, A. Kalmykov, A. Wissgott, G. Brandt, C. Jeong, O. Cheronet, M. Ferry, E. Harney, D. Keating, S. Mallick, N. Rohland, K. Stewardson, A. R. Kantorovich, V. E. Maslov, V. G. Petrenko, V. R. Erlikh, B. C. Atabiev, R. G. Magomedov, P. L. Kohl, K. W. Alt, S. L. Pichler, C. Gerling, H. Meller, B. Vardanyan, L. Yeganyan, A. D. Rezepkin, D. Mariaschk, N. Berezina, J. Gresky, K. Fuchs, C. Knipper, S. Schiffels, E. Balanovska, O. Balanovsky, I. Mathieson, T. Higham, Y. B. Berezin, A. Buzhilova, V. Trifonov, R. Pinhasi, A. B. Belinskij, D. Reich, S. Hansen, J. Krause, and W. Haak. 2019. Ancient human genome-wide data from a 3000-year interval in the Caucasus corresponds with ecogeographic regions. Nature Communications 10: 590.
Waples, R., A. Albrechtsen, and I. Moltke. 2019. Allele frequency-free inference of close familial relationships from genotypes or low-depth sequencing data. Molecular Ecology 28: 35–48.
Weir, B. S., A. D. Anderson, and A. B. Hepler. 2006. Genetic relatedness analysis: Modern data and new challenges. Nature Reviews Genetics 7: 771–780.
Zhu, X., S. Li, R. S. Cooper, and R. C. Elston. 2008. A unified association analysis approach for family and unrelated samples correcting for stratification. American Journal of Human Genetics 82: 352–365.